题目内容
 如图,已知:E为菱形ABOP的对角线的交点,C为AP上一点,连接BC交AO于D,且AD=AC.
如图,已知:E为菱形ABOP的对角线的交点,C为AP上一点,连接BC交AO于D,且AD=AC.
(1)求证:AE= (AB+AC);
(AB+AC);
(2)若AC=3,AB=5,求三角形ABD的面积.
(1)证明:∵四边形ABOP是菱形,
∴AB=OB,AC∥OB,AE= AO.
AO.
∴∠ACD=∠DBO.
∵AD=AC,∠ADC=∠BDO,
∴∠DBO=∠BDO.
∴AB=OB=OD.
∴AE= AO=
AO= (OD+AD)=
(OD+AD)= (AB+AC).
(AB+AC).
(2)解:AE= (AB+AC)=
(AB+AC)= (5+3)=4,
(5+3)=4,
BE= ,
,
S△ABD= AD•BE=4.5.
AD•BE=4.5.
分析:(1)求证AB=OD即可;
(2)利用(1)可求得AE,再由勾股定理求得BE,就可求得△ABD的面积.
点评:本题考查菱形的性质,平行线的性质,勾股定理,三角形的面积公式的理解及运用.
∴AB=OB,AC∥OB,AE=
 AO.
AO.∴∠ACD=∠DBO.
∵AD=AC,∠ADC=∠BDO,
∴∠DBO=∠BDO.
∴AB=OB=OD.
∴AE=
 AO=
AO= (OD+AD)=
(OD+AD)= (AB+AC).
(AB+AC).(2)解:AE=
 (AB+AC)=
(AB+AC)= (5+3)=4,
(5+3)=4,BE=
 ,
,S△ABD=
 AD•BE=4.5.
AD•BE=4.5.分析:(1)求证AB=OD即可;
(2)利用(1)可求得AE,再由勾股定理求得BE,就可求得△ABD的面积.
点评:本题考查菱形的性质,平行线的性质,勾股定理,三角形的面积公式的理解及运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知:E为菱形ABOP的对角线的交点,C为AP上一点,连接BC交AO于D,且AD=AC.
如图,已知:E为菱形ABOP的对角线的交点,C为AP上一点,连接BC交AO于D,且AD=AC. (2013•临汾二模)如图,已知四边形ABCD为菱形,对角线AC=6,BD=8,将△AOB沿射线AD的方向平移,平移的距离为线段AD的长,平移后得△DEC,则四边形ACED的周长等于( )
(2013•临汾二模)如图,已知四边形ABCD为菱形,对角线AC=6,BD=8,将△AOB沿射线AD的方向平移,平移的距离为线段AD的长,平移后得△DEC,则四边形ACED的周长等于( )
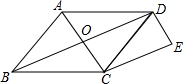 如图,已知四边形ABCD为菱形,对角线AC=6,BD=8,将△AOB沿射线AD的方向平移,平移的距离为线段AD的长,平移后得△DEC,则四边形ACED的周长等于
如图,已知四边形ABCD为菱形,对角线AC=6,BD=8,将△AOB沿射线AD的方向平移,平移的距离为线段AD的长,平移后得△DEC,则四边形ACED的周长等于