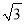题目内容
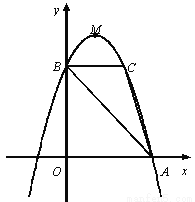
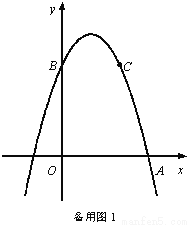
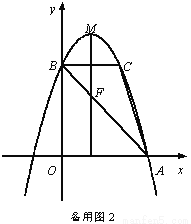
如图,抛物线y=ax 2+bx+c的顶点为M(1,4),与x轴的右交点为A,与y轴的交点为B,点C与点B关于抛物线的对称轴对称,且S△ABC =3.
(1)求抛物线的解析式;
(2)点D是y轴上一点,将点D绕C点逆时针旋转90°得到点E,若点E恰好落在抛物线上,请直接写出点D的坐标;
(3)设抛物线的对称轴与直线AB交于点F,问:在x轴上是否存在点P,使得以P、A、F为顶点的三角形与△ABC相似?若存在,求点P的坐标;若不存在,请说明理由
练习册系列答案
相关题目

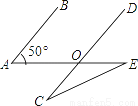
 D. 1+
D. 1+