题目内容
已知:O是线段AB的中点,直线MN经过点O,点C,D在直线MN上,∠1=∠2=45°.
(1)若点C与点O重合【图(1)】,请直接写出AC与BD的数量关系和位置关系;
(2)若点C,D不与点O重合【图(2)】,求证:AC=BD,AC⊥BD.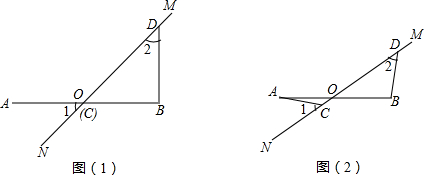
(1)若点C与点O重合【图(1)】,请直接写出AC与BD的数量关系和位置关系;
(2)若点C,D不与点O重合【图(2)】,求证:AC=BD,AC⊥BD.
考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)易证∠BOD=45°,即可证明BO=BD,OB⊥BD,易证AO=BO,即可求得AO=BD,即可解题;
(2)过B作BE⊥BD交OD于点E,易证∠BED=45°,可得AC⊥BD,∠OEB=∠ACO=135°,即可证明△ACO≌△BEO,可得AC=BE,即可解题.
(2)过B作BE⊥BD交OD于点E,易证∠BED=45°,可得AC⊥BD,∠OEB=∠ACO=135°,即可证明△ACO≌△BEO,可得AC=BE,即可解题.
解答:证明:(1)∵∠1=∠2=45°,
∴∠BOD=∠2=45°,
∴∠OBD=90°,BO=BD,
∴OB⊥BD,
∵O是线段AB的中点,
∴AO=BO,
∴AO=BD,且AO⊥BD;
(2)过B作BE⊥BD交OD于点E,

∵∠1=∠2=45°,BE⊥BD,
∴∠BED=∠2=45°,
∴BE=BD,∠OEB=∠ACO=135°,
∴AC∥BE,
∵BE⊥BD,
∴AC⊥BD,
在△ACO和△BEO中,
,
∴△ACO≌△BEO,(AAS)
∴AC=BE,
∴AC=BD.
∴∠BOD=∠2=45°,
∴∠OBD=90°,BO=BD,
∴OB⊥BD,
∵O是线段AB的中点,
∴AO=BO,
∴AO=BD,且AO⊥BD;
(2)过B作BE⊥BD交OD于点E,

∵∠1=∠2=45°,BE⊥BD,
∴∠BED=∠2=45°,
∴BE=BD,∠OEB=∠ACO=135°,
∴AC∥BE,
∵BE⊥BD,
∴AC⊥BD,
在△ACO和△BEO中,
|
∴△ACO≌△BEO,(AAS)
∴AC=BE,
∴AC=BD.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ACO≌△BEO是解题的关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
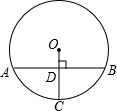 如图,在⊙O中,OC垂直弦AB于点D,交⊙O于点C,若AB=24,半径OC=13,则CD的长是
如图,在⊙O中,OC垂直弦AB于点D,交⊙O于点C,若AB=24,半径OC=13,则CD的长是 已知△ABC与△DEF是全等三角形,试分析△ABC怎样变化才能得到△DEF.
已知△ABC与△DEF是全等三角形,试分析△ABC怎样变化才能得到△DEF.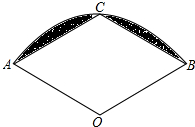 如图,在扇形AOB中,半径OA=1,∠AOB=120°,C为弧AB的中点,连接AC、BC,则图中阴影部分的面积是
如图,在扇形AOB中,半径OA=1,∠AOB=120°,C为弧AB的中点,连接AC、BC,则图中阴影部分的面积是