Question

在△ABC中，cosB=

1

2

，∠C=45°，AB=8，以点B为圆心4为半径的⊙B与以点C为圆心的⊙C相切，则⊙C的半径为

 

．

Answer 1

分析：由cosB=

1

2

，可以确定∠B=60°，由于∠C=45°，AB=8，过点A作三角形的高，易确定BC=4+4

3

，已知两圆相切，应分内切和外切两种情况分类讨论．

解答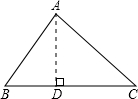：解：根据题意画出图形如图示，
过点A作DA⊥BC于点D，
∴∠ADB=∠ADC=90°，
∵cosB=

1

2

，
∴∠B=60°，
∴∠BAD=30°，
∵AB=8，
∴BD=

1

2

×8=4，AD=4

3

，
∵∠C=45°，
∴∠BAC=45°，
∴AD=DC=4

3

，
∴BC=4+4

3

，
∵以点B为圆心4为半径的⊙B与以点C为圆心的⊙C相切，
设两圆的圆心距为d，⊙C的半径为r，
∴当两圆外切时，两圆的圆心距d=4+r，
即4+4

3

=4+r，解得r=4

3

．
当两圆内切时，两圆的圆心距d=r-4，
即4+4

3

=r-4，解得r=8+4

3

．
故答案为：4

3

或8+4

3

．

点评：本题考查了圆与圆的位置关系，熟记两圆半径与圆心距之间的数量关系是解题的关键．外离：则P＞R+r；外切：则P=R+r；相交：则R-r＜P＜R+r；内切：则P=R-r；内含：则0≤P＜R-r．（P表示圆心距，R，r分别表示两圆的半径）．