题目内容
5. 如图,平行四边形ABCD中,E、F是对角线AC上的两点,∠DEF=∠EFB.
如图,平行四边形ABCD中,E、F是对角线AC上的两点,∠DEF=∠EFB.(1)求证:AE=CF;
(2)求证:四边形EBFD是平行四边形.
分析 (1)由四边形ABCD为平行四边形得出AD=BC,∠DAE=∠BCF,由∠DEF=∠EFB,得出∠AED=∠CFB,DE∥BF,由AAS证得△AED≌△CFB,即可得出结论;
(2)由△AED≌△CFB,得出DE=BF,即可得出结论.
解答 证明:(1)∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,
∴∠DAE=∠BCF,
∵∠DEF=∠EFB,
∴∠AED=∠CFB,DE∥BF,
在△AED与△CFB中,
$\left\{\begin{array}{l}{∠AED=∠CFB}\\{∠DAE=∠BCF}\\{AD=BC}\end{array}\right.$,
∴△AED≌△CFB(AAS),
∴AE=CF;
(2)∵△AED≌△CFB,
∴DE=BF,
∵DE∥BF,
∴四边形EBFD为平行四边形.
点评 本题考查了平行四边形的判定与性质、全等三角形的判定与性质、平行线的判定定理等知识;熟练掌握平行四边形的判定与性质、全等三角形的判定与性质是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,EF∥AD,∠1=∠2,∠BAC=60°,求∠AGD的度数.
如图,EF∥AD,∠1=∠2,∠BAC=60°,求∠AGD的度数. 如图,已知在△ABC中,点D、E分别是AB、AC上一点,且AD=AE,∠ABE=∠ACD,BE与CD相交于点F.试判断△BCF的形状,并说明理由.
如图,已知在△ABC中,点D、E分别是AB、AC上一点,且AD=AE,∠ABE=∠ACD,BE与CD相交于点F.试判断△BCF的形状,并说明理由. 如图,在等腰△ABC中,腰长AB=AC=8厘米,底边BC=6厘米,点D为AB的中点.如果点M在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点N在线段CA上由C点向A点运动.当点N的运动速度为2或$\frac{8}{3}$厘米/秒时,能够使△BMD与△CNM全等.
如图,在等腰△ABC中,腰长AB=AC=8厘米,底边BC=6厘米,点D为AB的中点.如果点M在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点N在线段CA上由C点向A点运动.当点N的运动速度为2或$\frac{8}{3}$厘米/秒时,能够使△BMD与△CNM全等. 某商店经销甲、乙两种商品.请您根据图中所给的信息解答下列问题:
某商店经销甲、乙两种商品.请您根据图中所给的信息解答下列问题: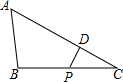 如图,在△ABC中,∠ABC>90°,∠C=30°,BC=12,P是BC上的一个动点,过点P作PD⊥AC于点D,设CP=x,△CDP的面积为y,则y与x之间的函数图象大致为( )
如图,在△ABC中,∠ABC>90°,∠C=30°,BC=12,P是BC上的一个动点,过点P作PD⊥AC于点D,设CP=x,△CDP的面积为y,则y与x之间的函数图象大致为( )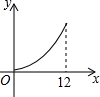
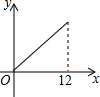
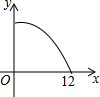
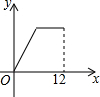
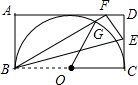 如图,在矩形ABCD中,BC=12,以BC为直径的半圆O恰好与AD相切,现将矩形ABCD沿BE折叠,使点C落在边AD的点F处,并交半圆O于点G,则扇形OCG的面积为( )
如图,在矩形ABCD中,BC=12,以BC为直径的半圆O恰好与AD相切,现将矩形ABCD沿BE折叠,使点C落在边AD的点F处,并交半圆O于点G,则扇形OCG的面积为( )