题目内容
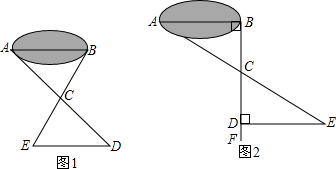
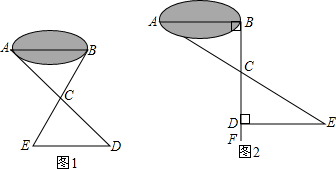
如图所示,为在池塘两侧A、B两处架桥,要知道无法测量的A、B两点的距离,找一处看得见A、B的点P.

(1)连结AP并延长到D,使PA=PD,连结BP,并延长到C,使PC=PB.测得CD=35m,就确定了AB也是35m,说明其中的理由;
(2)也可先过B点作AB的垂线BF,再在BF上取C、D两点,使BC=CD.接着过点D作BD的垂线DE交AC的延长线于E,则测出DE的长即为A、B的距离.你认为这种方案是否切实可行,请说出你的理由.作BD⊥AB,ED⊥BF的目的是什么?若满足∠ABD=∠BDE≠![]() ,此方案是否仍然可行?为什么?
,此方案是否仍然可行?为什么?
答案:
解析:
解析:
|
(1)∵PA=PD ∠APB=∠CPD PC=PB ∴△APB≌△CPC(SAS),∴AB=CD ∵CD=35m ∴AB=35m. (2)根据ASA可证△ACB≌△ECD ∴AB=DE.若∠ABC=∠EDC≠ 分析:(1)由题给的条件知△APB≌△CPD,∴CD=AB.这样就可知A、B两点的距离了. (2)是探究式题目,作两个垂直线段的目的是为了找AB∥DE.若不是垂直,这个方案也可行,同样利用ASA完成. |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
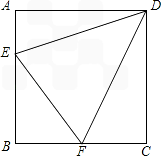
 如图所示,友芝村有一口呈四边形的池塘,在它的四个角A、B、C、D处均种有一棵大核桃树,该村准备挖池塘建养鱼池,要使建后的鱼池面积为原池塘面积的两倍,又想保证树不动,并要求建后的池塘成平行四边形形状.请问友芝村能否实现这一设想?若能,请你设计并画出图形,若不能,请说明理由(画图保留作图痕迹,不写画法).
如图所示,友芝村有一口呈四边形的池塘,在它的四个角A、B、C、D处均种有一棵大核桃树,该村准备挖池塘建养鱼池,要使建后的鱼池面积为原池塘面积的两倍,又想保证树不动,并要求建后的池塘成平行四边形形状.请问友芝村能否实现这一设想?若能,请你设计并画出图形,若不能,请说明理由(画图保留作图痕迹,不写画法).