Question

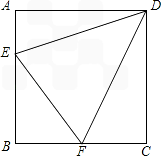
如图所示，一个正方形池塘边长为12m，在池塘边AB上的点E处有一颗果树，池塘边BC上的点F处也有一颗果树，两颗果树的距离EF=AE+FC．
（1）你能知道这两颗果树之间的距离吗？算算看！
（2）试着求出∠EDF的度数．

Answer 1

解：如图，将△ADE逆时针旋转90°， 使得AD、DC重合，得到△DCG； 则CG=AE，EF=FG=AE+CF； 又∵DE=DG，DF=DF， ∴△DEF△DGF（SSS）； （1）设AE=x，CF=y； 则BE=12﹣x，BF=12﹣y，EF=x+y； 在Rt△BEF中，由勾股定理得： （12﹣x）2+（12﹣y）2=（x+y）2， 解得：xy+12（x+y）=144， 两个未知数一个方程，不能确定x+y的取值， 故EF为非定值； （2）由△DEF△DGF，得：∠EDF=∠FDG； 而∠EDG=∠EDC+∠CDG=∠EDC+ADE=90°， 则∠EDF=45°．