题目内容
解方程:
-1=
.
| x |
| x-1 |
| 3 |
| x2-1 |
考点:解分式方程
专题:计算题
分析:方程两边都乘以最简公分母(x+1)(x-1)化为整式方程,然后解方程即可,最后进行检验.
解答:解:方程两边都乘以(x+1)(x-1)去分母得,
x(x+1)-(x2-1)=3,
即x2+x-x2+1=3,
解得x=2
检验:当x=2时,(x+1)(x-1)=(2+1)(2-1)=3≠0,
∴x=2是原方程的解,
故原分式方程的解是x=2.
x(x+1)-(x2-1)=3,
即x2+x-x2+1=3,
解得x=2
检验:当x=2时,(x+1)(x-1)=(2+1)(2-1)=3≠0,
∴x=2是原方程的解,
故原分式方程的解是x=2.
点评:本题考查了分式方程的求解,(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.
(2)解分式方程一定注意要验根.
(2)解分式方程一定注意要验根.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
把足够大的一张厚度为0.1mm的纸连续对折,要使对折后的整叠纸总厚度超过20mm,至少要对折( )
| A、6次 | B、7次 | C、8次 | D、9次 |
 某班的元旦晚会上,有一个转盘摇奖游戏.如图有甲、乙两个转盘,参与者只能选择其中的一个.当转盘停止时,指针落在哪一区域就可获得相应的奖品.如果小颖想得到“铅笔”,她应选择( )
某班的元旦晚会上,有一个转盘摇奖游戏.如图有甲、乙两个转盘,参与者只能选择其中的一个.当转盘停止时,指针落在哪一区域就可获得相应的奖品.如果小颖想得到“铅笔”,她应选择( )| A、乙转盘 |
| B、甲转盘 |
| C、甲、乙转盘均可 |
| D、无法选择哪个转盘 |
 已知电流在一定时间段内正常通过电子元件
已知电流在一定时间段内正常通过电子元件 的概率是0.5,则一定时间段内,A、B之间电流能够正常通过的概率是( )
的概率是0.5,则一定时间段内,A、B之间电流能够正常通过的概率是( )(提示:在一次试验中,每个电子元件的状态有两个可能(通电,断开),并且这两种状态的可能性相等.)
A、
| ||
B、
| ||
C、
| ||
| D、1 |
下列命题中,逆命题是真命题的是( )
| A、如果a=b,那么a2=b2 | ||
| B、在一元二次方程ax2+bx+c=0(a≠0)中,如果方程有两个相等的实数根,那么△=0 | ||
| C、长方形既是轴对称图形又是中心对称图形 | ||
D、在反比例函数y=
|

 如图,已知△ABC,图中的每个小正方形的边长为1;
如图,已知△ABC,图中的每个小正方形的边长为1;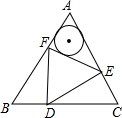 已知:如图,边长为a的正△ABC内有一边长为b的正△DEF,且a-b=2,则△AEF的内切圆半径为
已知:如图,边长为a的正△ABC内有一边长为b的正△DEF,且a-b=2,则△AEF的内切圆半径为