Question

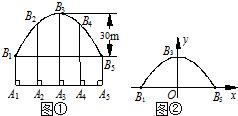
如图所示，图①是一座抛物线型拱桥在建造过程中装模时的设计示意图，拱高为30m，支柱A₃B₃=50m，5根支柱A₁B₁、A₂B₂、A₃B₃、A₄B₄、A₅B₅之间的距离均为15m，B₁B₅∥A₁A₅，将抛物线放在图②所示的直角坐标系中．
（1）直接写出图②中点B₁、B₃、B₅的坐标；
（2）求图②中抛物线的函数表达式；
（3）求图①中支柱A₂B₂、A₄B₄的长度．

Answer 1

分析：（1）由题目中的数据直接写出点的坐标即可；
（2）设出二次函数的交点式，代入点B₃的坐标解答即可；
（3）代入B2、B4的横坐标，求出纵坐标，即可解决问题．

解答：解：（1）B₁（-30，0），B₃（0，30），B₅（30，0）；

（2）设抛物线的表达式为y=a（x-30）（x+30），
把B₃（0，30）代入得y=a（0-30）（0+30）=30，
解得a=-

1

30

，
所求抛物线的表达式为：y=-

1

30

(x-30)(x+30)；

（3）∵B₄点的横坐标为15，
∴B₄的纵坐标y4=-

1

30

(15-30)(15+30)=

45

2

，
∵A₃B₃=50，拱高为30，
∴立柱A₄B₄=20+

45

2

=

85

2

（米）；
由对称性知：A2B2=A4B4=

85

2

（米）．

点评：此题考查待定系数法求函数解析式、二次函数的对称性以及利用解析式求点的坐标等问题．