Question

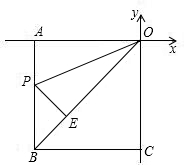如图，若正方形ABCO的各顶点的坐标为A（-2，0），B（-2，-2），C（0，-2），O（0，0），把正方形沿OP对折，使点A落在对角线OB上的E处，折痕交AB于E，试求△EPO的面积．

Answer 1

分析：由已知可得AO=AB=2，可求得OB的大小，根据折叠，找到相等的量，利用OB列出方程可得到AP的大小，从而求得三角形的面积．

解答：解：∵A（-2，0），B（-2，-2），
∴AO=AB=2，
∴OB=

AO2+AB2

=

22+22

=2

2

，
设AP=x，OP为折痕，
∴PE=AP=x，OE=AO=2，∠OAP=∠PEO=90°，
OB为对角线，
∴∠2=45°，
∴∠1=∠2=45°，
BE=PE=x，
∴x+2=2

2

，
∴x=2

2

-2，
∴△EPO的面积为：

1

2

×2×（2

2

-2）=2

2

-2．

点评：本题考查了翻折问题、坐标与图形的性质及勾股定理；找着相等的角、相等的边是正确解答本题的关键．