��Ŀ����
1���������κ���y1=ax2+bx+c��һ�κ���y2=kx+m��ͼ��ʱ�����г��±���| x | �� | -1 | 0 | 1 | 2 | 3 | 4 | 5 | �� |
| y1 | �� | 0 | -3 | -4 | -3 | 0 | 5 | 12 | �� |
| y2 | �� | 0 | 2 | 4 | 6 | 8 | 10 | 12 | �� |
��1�����κ���y1=ax2+bx+c��ͼ����y�ύ������Ϊ��0��-3����
��2����y1��y2ʱ���Ա���x��ȡֵ��Χ��x��-1��x��5��
��3����д�����κ���y1=ax2+bx+c��������ͬ�����ʣ�
���� ��1����x=0�����y����ֵ��ȷ����y�ύ�����꼴�ɣ�
��2�������ô���ϵ����������κ�����һ�κ����Ľ���ʽ�����������ͼ��Ľ��㣬�����ɵó����ۣ�
��3�����ö��κ��������ʣ����ڷ��Գ��ᣬ������ֱ�ӵó��𰸼��ɣ�
��� �⣺��1�����κ���y1=ax2+bx+c��ͼ����y�ύ������Ϊ��0��-3����
��2��������ã�
$\left\{\begin{array}{l}{a-b+c=0}\\{c=-3}\\{a+b+c=-4}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=1}\\{b=-2}\\{c=-3}\end{array}\right.$��
����κ����Ľ���ʽΪy=x2-2x-3=��x-1��2-4��
��һ�κ���y2=kx+m��ͼ����㣨-1��0������0��2����
��$\left\{\begin{array}{l}{-k+m=0}\\{m=2}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=2}\\{m=2}\end{array}\right.$��
��һ�κ����Ľ���ʽΪy=2x+2��
��ͼ��ʾ��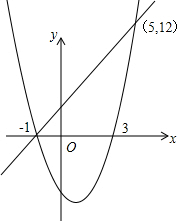
��x��-1��x��5ʱ�����κ�����ֵ����һ�κ�����ֵ��
��3���ú�����ͼ�����ϣ���x=1ʱ�����������ֵ����x��1ʱ��y��x���������С����x��1ʱ��y��x�����������������Ϊ��1��-4�����Գ���Ϊֱ��x=1��
���� ���⿼����κ��������ʣ�����ϵ������������ʽ�����ͼ�����ö��κ��������ʽ�����⣮

 �ִʾ��ƪϵ�д�
�ִʾ��ƪϵ�д� ��ͼ����֪��AOB=90�㣬����O��ֱ��CD����OE��CD�ڵ�O��
��ͼ����֪��AOB=90�㣬����O��ֱ��CD����OE��CD�ڵ�O�� ABΪ��ԲO��ֱ�����ֽ�һ�����ֱ�����ǰ���ͼ���ã���Ƕ���P�ڰ�Բ�ϣ�б�߹���B��һ��ֱ�DZ߽��ð�Բ�ڵ�Q����AB=2�����߶�BQ�ij�Ϊ$\sqrt{2}$��
ABΪ��ԲO��ֱ�����ֽ�һ�����ֱ�����ǰ���ͼ���ã���Ƕ���P�ڰ�Բ�ϣ�б�߹���B��һ��ֱ�DZ߽��ð�Բ�ڵ�Q����AB=2�����߶�BQ�ij�Ϊ$\sqrt{2}$�� ��1��һ������γ���һ���ڽ��⣬������ڽ�֮����3120�㣬����һ�ڽǵĶ���������εı���
��1��һ������γ���һ���ڽ��⣬������ڽ�֮����3120�㣬����һ�ڽǵĶ���������εı��� ��ͼ����֪��C���߶�AB�ϣ���M��N�ֱ���AC��BC���е㣬��AB=8cm����MN�ij���Ϊ��������cm��
��ͼ����֪��C���߶�AB�ϣ���M��N�ֱ���AC��BC���е㣬��AB=8cm����MN�ij���Ϊ��������cm��