题目内容
直线y=x+2与双曲线
（k＞0）在第一象限内交于点P（a，b），且1≤a≤2，则k的取值范围是________．
3≤k≤8
分析：两函数图象相交于一点，把该点代入一次函数解析式，求出a、b的关系，然后再代入双曲线中求出k的取值范围．
解答：∵直线y=x+2与双曲线（k＞0）在第一象限内交于点P（a，b），
∴
，
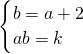∴k=a（a+2），
∵1≤a≤2，
∴3≤k≤8．
故答案为：3≤k≤8．
点评：本题主要考查两函数图象交点的问题和解不等式等知识点，涉及的知识面较广，应重点掌握．
分析：两函数图象相交于一点，把该点代入一次函数解析式，求出a、b的关系，然后再代入双曲线中求出k的取值范围．
解答：∵直线y=x+2与双曲线
（k＞0）在第一象限内交于点P（a，b），∴
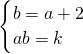，∴k=a（a+2），
∵1≤a≤2，
∴3≤k≤8．
故答案为：3≤k≤8．
点评：本题主要考查两函数图象交点的问题和解不等式等知识点，涉及的知识面较广，应重点掌握．
练习册系列答案
相关题目
x，y轴平行，纸板的另两个顶点A，B恰好是直线y=kx+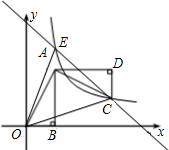
绕点A逆时针旋转90°，点O的对应点C恰好落在双曲线y=
如图，直线y=mx+n与双曲线y=
如图，直线y=-2x-2与双曲线
如图，直线y1=mx+n与双曲线