题目内容
如图,在边长为2的等边△ABC中,AD⊥BC,点P为边AB 上一个动点,过P点作PF//AC交线段BD于点F,作PG⊥AB交AD于点E,交线段CD于点G,设BP=x.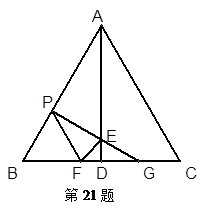
(1)①填空:如果BP=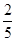 ,则BG= ;
,则BG= ;
②用x的代数式表示线段DG的长,并直接写出自变量x的取值范围;
(2)记△DEF的面积为S,求S与x之间的函数关系式。
(3)当以P、E、F为顶点的三角形与△EDG相似时,请求出BP的长。
(1)BG=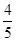 ;DG=2x-1、
;DG=2x-1、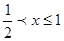 (2)S=
(2)S=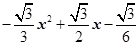 (3)
(3)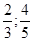
解析试题分析:(1)①在边长为2的等边△ABC中,所以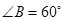 ;作PG⊥AB交AD于点E,交线段CD于点G,
;作PG⊥AB交AD于点E,交线段CD于点G,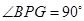 ,在三角形BPG中,由三角形内角和定理知
,在三角形BPG中,由三角形内角和定理知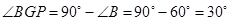 ,因为BP=
,因为BP=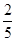 ,所以BG=
,所以BG=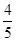
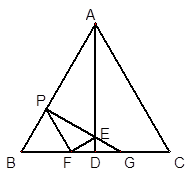
②∵PF//AC,∴△PBF为等边三角形,∴BF=PF=PB=x.
又∵BG=2x,BD=1,∴DG=2x-1,∴0<2x-1≤1,∴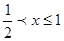 .
.
(2)S=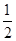 DE×DF=
DE×DF=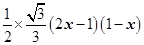
=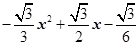
(3)①如图1,若∠PFE=∠EDG=90 ,∵∠EGD =∠FPE ∴
,∵∠EGD =∠FPE ∴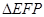 ∽△EDG,∴∠EFD=∠EGD=30
∽△EDG,∴∠EFD=∠EGD=30 ∴EF=EG
∴EF=EG
∵AD⊥BC ∴DF=DG 即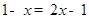 解得:
解得: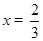 .
.
②如图2,若∠PEF=∠EDG=90 时,∵∠EGD =∠FPE ∴
时,∵∠EGD =∠FPE ∴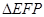 ∽△DEG
∽△DEG
∵∠FED=30
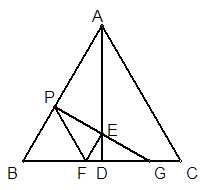
∴DF=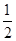 EF=
EF=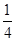 BP,
BP,
即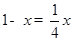 .解得:
.解得: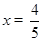
考点:直角三角形,等边三角形,相似三角形
点评:本题考查直角三角形,等边三角形,相似三角形,解答本题需要掌握直角三角形,等边三角形的性质,熟悉相似三角形的证明方法,会证明两个三角形相似

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 如图,在边长为4的等边三角形ABC中,AD是BC边上的高,点E,F是AD上的两点,则图中阴影部分的面积是( )
如图,在边长为4的等边三角形ABC中,AD是BC边上的高,点E,F是AD上的两点,则图中阴影部分的面积是( )A、4
| ||
B、3
| ||
C、2
| ||
D、
|
 如图,在边长为20cm的等边三角形ABC纸片中,以顶点C为圆心,以此三角形的高为半径画弧分别交AC、BC于点D、E,则扇形CDE所围的圆锥(不计接缝)的底圆半径为( )
如图,在边长为20cm的等边三角形ABC纸片中,以顶点C为圆心,以此三角形的高为半径画弧分别交AC、BC于点D、E,则扇形CDE所围的圆锥(不计接缝)的底圆半径为( )A、
| ||||
B、
| ||||
C、5
| ||||
D、10
|
 如图,在边长为1的等边三角形ABC中,若将两条含120°圆心角的
如图,在边长为1的等边三角形ABC中,若将两条含120°圆心角的
 交AD于点E,交线段CD于点G,设BP=x.
交AD于点E,交线段CD于点G,设BP=x. (2013•武汉模拟)如图,在边长为1的等边△OAB中,以边AB为直径作⊙D,以O为圆心OA长为半径作圆O,C为半圆AB上不与A、B重合的一动点,射线AC交⊙O于点E,BC=a,AC=b.
(2013•武汉模拟)如图,在边长为1的等边△OAB中,以边AB为直径作⊙D,以O为圆心OA长为半径作圆O,C为半圆AB上不与A、B重合的一动点,射线AC交⊙O于点E,BC=a,AC=b.