题目内容
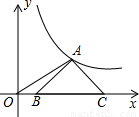
 如图,等腰Rt△OAB中∠OAB=90°,顶点O为坐标原点,顶点A、B在某反比例函数的图象上,点A的横坐标为2,则S△OAB=________.
如图,等腰Rt△OAB中∠OAB=90°,顶点O为坐标原点,顶点A、B在某反比例函数的图象上,点A的横坐标为2,则S△OAB=________.
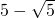
分析:首先根据已知构造矩形,得出△AON≌△BAW,进而得出矩形面积为:S=ON•WN=2(2+
 )=4+k,再利用S△AOB=4+k-3×
)=4+k,再利用S△AOB=4+k-3× =4-
=4- ,进而利用AO=AB,再表示出即可得出S△AOB=
,进而利用AO=AB,再表示出即可得出S△AOB= ×
×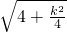 ×
×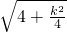 =2+
=2+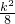 ,再利用两三角形面积相等得出k的值,即可得出答案.
,再利用两三角形面积相等得出k的值,即可得出答案.解答:
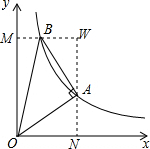 解:过点B作BM⊥y轴于点M,过点A作AN⊥x轴于点N,并延长MB,NA交于一点W,
解:过点B作BM⊥y轴于点M,过点A作AN⊥x轴于点N,并延长MB,NA交于一点W,∵∠WMO=∠MON=∠WNO=90°,
∴四边形MONW是四边形,
设反比例函数的解析式为:y=
 ,
,由点A的横坐标为2,则A点坐标为:(2,
 ),
),∵等腰Rt△OAB中,∠OAB=90°,
∴AB=AO,
∵∠OAB=90°,
∴∠BAW+∠OAN=90°,
∵∠AON+∠OAN=90°,
∴∠BAW=∠AON,
∵在△AON和△BAW中,
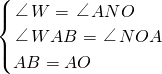 ,
,∴△AON≌△BAW(AAS),
∴AW=NO,S△AON=S△BAW,
故WN=AW+AN=2+
 ,
,∴矩形面积为:S=ON•WN=2(2+
 )=4+k,
)=4+k,∵S△MOB=S△AON=S△BAW=
 ×2×
×2× =
= ,
,∴S△AOB=4+k-3×
 =4-
=4- ,
,∵NO=2,AN=
 ,
,∴AB=AO=
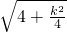 ,
,∴S△AOB=
 ×
×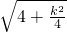 ×
×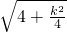 =2+
=2+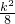 ,
,∴4-
 =2+
=2+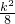 ,
,整理得出:
k2+4k-16=0,
解得:k1=-2+2
 ,k2=-2-2
,k2=-2-2 (不合题意舍去),
(不合题意舍去),∴S△AOB=4-
 =4-
=4-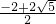 =5-
=5- .
.故答案为:5-
 .
.点评:此题主要考查了反比例函数的综合应用以及全等三角形的判定与性质以及三角形面积求法等知识,根据已知用两种方法得出S△AOB是解题关键.

练习册系列答案
相关题目
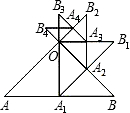 已知:如图,等腰Rt△OAB的直角边OA的长为1,以AB边上的高OA1为直角边,按逆时针方向作等腰Rt△OA1B1,A1B1与OB相交于点A2.若再以OA2为直角边按逆时针方向作等腰Rt△OA2B2,A2B2与OB1相交于点A3,按此作法进行下去,得到△OA3B3,△OA4B4,…,则△OA6B6的周长是
已知:如图,等腰Rt△OAB的直角边OA的长为1,以AB边上的高OA1为直角边,按逆时针方向作等腰Rt△OA1B1,A1B1与OB相交于点A2.若再以OA2为直角边按逆时针方向作等腰Rt△OA2B2,A2B2与OB1相交于点A3,按此作法进行下去,得到△OA3B3,△OA4B4,…,则△OA6B6的周长是 如图,等腰Rt△ABC的斜边BC在x轴上,顶点A在反比例函数
如图,等腰Rt△ABC的斜边BC在x轴上,顶点A在反比例函数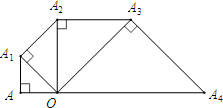 如图,等腰Rt△OAA1的直角边OA长为1.
如图,等腰Rt△OAA1的直角边OA长为1.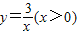 的图象上,连接OA,则OC2-OA2= .
的图象上,连接OA,则OC2-OA2= .