题目内容
1.已知AB是⊙O的直径,P为AB延长线上的任意一点,过点P作⊙O的切线,切点为C,∠APC的平分线PD与AC交于点D.(1)如图①,若∠CPA恰好等于30°,求∠CDP的度数;
(2)如图②,若∠CPA不等于30°时,①中的结论是否仍然成立?请说明理由.

分析 (1)利用切线的性质得出∠OCP=90°,进而利用∠CPA=30°,得出∠COP的度数,进而结合角平分线的性质得出∠APD,再利用∠CDP=∠A+∠APD求出答案;
(2)利用切线的性质得出∠OCP=90°,结合角平分线的性质得出∠APC=2∠APD,结合∠COP=2∠A,得出2(∠A+∠APD)=90°,进而求出答案.
解答 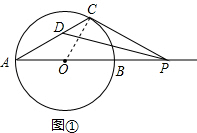 解:(1)如图①,连接OC,
解:(1)如图①,连接OC,
∵直线PC是⊙O的切线,
∴OC⊥PC,则∠OCP=90°,
∵∠CPA=30°,
∴∠COP=90°-30°=60°,
∵OA=OC,
∴∠A=∠ACO=30°,
∵PD平分∠APC,
∴∠APD=$\frac{1}{2}$×30°=15°,
∴∠CDP=∠A+∠APD=30°+15°=45°,
即∠CDP的度数为:45°;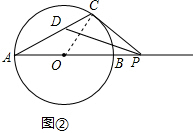
(2)∠CDP的大小不发生变化,
理由:如图②,连接CO,
∵PC是⊙O的切线,
∴∠OCP=90°,
∵PD是∠CPA的平分线,
∴∠APC=2∠APD,
∵OA=OC,
∴∠A=∠ACO,
∴∠COP=2∠A,
∴∠COP+∠APC=90°,即2(∠A+∠APD)=90°,
∴∠CDP=∠A+∠APD=45°,
故∠CDP的大小不发生变化.
点评 此题主要考查了切线的性质以及角平分线的性质,正确得出2(∠A+∠APD)=90°是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.课间休息,小丽在玩抛掷两枚硬币的游戏,她掷出“两个正面朝上”的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
6.已知4y2+my+9是完全平方式,则m为( )
| A. | 6 | B. | ±6 | C. | ±12 | D. | 12 |
 如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AC=9,则CP的长为3.
如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AC=9,则CP的长为3. 如图,⊙O是△ABC的外接圆,BC是⊙O的直径,作∠CAD=∠B,且点D在BC延长线上.
如图,⊙O是△ABC的外接圆,BC是⊙O的直径,作∠CAD=∠B,且点D在BC延长线上. 如图,在△ABC中,BC=12cm,点M是∠ABC和∠ACB的角平分线的交点,且MD∥AB,ME∥AC,求△MDE的周长.
如图,在△ABC中,BC=12cm,点M是∠ABC和∠ACB的角平分线的交点,且MD∥AB,ME∥AC,求△MDE的周长. 如图,A、B是双曲线y=$\frac{k}{x}$上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C,若△ADO的面积为3,D为OB的中点,则k的值为8.
如图,A、B是双曲线y=$\frac{k}{x}$上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C,若△ADO的面积为3,D为OB的中点,则k的值为8.