题目内容
 如图,AB=AC,AB的垂直平分线DE交BC延长线于E,交AC于F,∠A=50°,AB+BC=6.
如图,AB=AC,AB的垂直平分线DE交BC延长线于E,交AC于F,∠A=50°,AB+BC=6.(1)△BCF的周长为多少?
(2)∠E的度数为多少?
考点:线段垂直平分线的性质,等腰三角形的性质
专题:
分析:(1)由AB的垂直平分线DE交BC延长线于E,交AC于F,根据线段垂直平分线的性质,可得AF=BF,即可得△BCF的周长为AC+BC,然后由AB=AC,AB+BC=6,求得答案;
(2)由AB=AC,∠A=50°,可求得∠ABC的度数,继而求得答案.
(2)由AB=AC,∠A=50°,可求得∠ABC的度数,继而求得答案.
解答:解:(1)∵DF是AB的垂直平分线
∴AF=BF,
∵AB+BC=6,AB=AC,
∴△BCF的周长为:BC+CF+BF=BC+CF+AF=BC+AC=AB+BC=6;
(2)∵AB=AC,∠A=40°,
∴∠ACB=∠ABC=
(180°-40°)=70°,
∵AB的垂直平分线DE交BC延长线于E,交AC于F,
∴∠BDE=90°,
∴∠E=90°-∠ABC=20°.
∴AF=BF,
∵AB+BC=6,AB=AC,
∴△BCF的周长为:BC+CF+BF=BC+CF+AF=BC+AC=AB+BC=6;
(2)∵AB=AC,∠A=40°,
∴∠ACB=∠ABC=
| 1 |
| 2 |
∵AB的垂直平分线DE交BC延长线于E,交AC于F,
∴∠BDE=90°,
∴∠E=90°-∠ABC=20°.
点评:此题考查了线段垂直平分线的性质以及等腰三角形的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
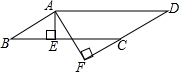 如图,在?ABCD中,AE⊥BC于点E,AF⊥CD交DC于DC的延长线于点F,AB=3cm,AF=7cm,∠EAF=30°,求∠B的度数和?ABCD周长.
如图,在?ABCD中,AE⊥BC于点E,AF⊥CD交DC于DC的延长线于点F,AB=3cm,AF=7cm,∠EAF=30°,求∠B的度数和?ABCD周长. 如图,添加必要的一个条件,使得AB∥CD,这个条件可以是
如图,添加必要的一个条件,使得AB∥CD,这个条件可以是 如图,由∠1=∠2,可以推出
如图,由∠1=∠2,可以推出 如图,如果∠1=40°,∠2=40°,∠3=40°,可判定哪些直线平行,请说明所用的判定方法.
如图,如果∠1=40°,∠2=40°,∠3=40°,可判定哪些直线平行,请说明所用的判定方法. 已知:如图,直线a,b,c被直线d所截,∠2=∠3,∠1+∠3=180°.找出图中的平行线,并给出证明.
已知:如图,直线a,b,c被直线d所截,∠2=∠3,∠1+∠3=180°.找出图中的平行线,并给出证明.