题目内容
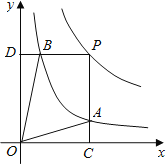
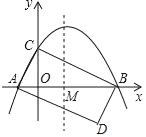
【题目】已知:如图1,抛物线的顶点为M,平行于x轴的直线与该抛物线交于点A,B(点A在点B左侧),根据对称性△AMB恒为等腰三角形,我们规定:当△AMB为直角三角形时,就称△AMB为该抛物线的“完美三角形”.

(1)①如图2,求出抛物线![]() 的“完美三角形”斜边AB的长;
的“完美三角形”斜边AB的长;
②抛物线![]() 与
与![]() 的“完美三角形”的斜边长的数量关系是 ;
的“完美三角形”的斜边长的数量关系是 ;
(2)若抛物线![]() 的“完美三角形”的斜边长为4,求a的值;
的“完美三角形”的斜边长为4,求a的值;
(3)若抛物线![]() 的“完美三角形”斜边长为n,且
的“完美三角形”斜边长为n,且![]() 的最大值为-1,求m,n的值.
的最大值为-1,求m,n的值.
【答案】(1)AB=2;相等;(2)a=±![]() ;(3)
;(3)![]() ,∴
,∴![]() .
.
【解析】
试题(1)过点B作BN⊥x轴于N,由题意可知△AMB为等腰直角三角形,设出点B的坐标为(n,-n),根据二次函数得出n的值,然后得出AB的值;(2)根据抛物线的性质相同得出抛物线的完美三角形全等,从而得出点B的坐标,得出a的值;根据最大值得出mn-4m-1=0,根据抛物线的完美三角形的斜边长为n得出点B的坐标,然后代入抛物线求出m和n的值.
试题解析:(1)①过点B作BN⊥x轴于N,由题意可知△AMB为等腰直角三角形,AB∥x轴,
易证MN=BN,设B点坐标为(n,-n),代入抛物线![]() ,得
,得![]() ,
,
∴![]() ,
,![]() (舍去),∴抛物线
(舍去),∴抛物线![]() 的“完美三角形”的斜边
的“完美三角形”的斜边![]()
②相等;
(2)∵抛物线![]() 与抛物线
与抛物线![]() 的形状相同,
的形状相同,
∴抛物线![]() 与抛物线
与抛物线![]() 的“完美三角形”全等,
的“完美三角形”全等,
∵抛物线![]() 的“完美三角形”斜边的长为4,∴抛物线
的“完美三角形”斜边的长为4,∴抛物线![]() 的“完美三角形”斜边的长为4,
的“完美三角形”斜边的长为4,
∴B点坐标为(2,2)或(2,-2),∴![]() .
.
(3)∵![]() 的最大值为-1,∴
的最大值为-1,∴![]() ,
,
∴![]() ,∵抛物线
,∵抛物线![]() 的“完美三角形”斜边长为n,
的“完美三角形”斜边长为n,
∴抛物线![]() 的“完美三角形”斜边长为n,∴B点坐标为
的“完美三角形”斜边长为n,∴B点坐标为![]() ,
,
∴代入抛物线![]() ,得
,得![]() ,∴
,∴![]() (不合题意舍去),
(不合题意舍去),
∴![]() ,∴
,∴![]()

【题目】数学课上,李老师出示了如下框中的题目.
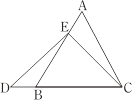
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图.试确定线段AE与DB的大小关系,并说明理由. |
|
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:
AE DB(填“>”,“<”或“=”).

图1 图2
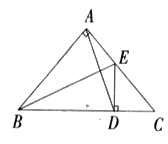
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F.
(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).
【题目】今年是“五四”运动![]() 周年,为进一步弘扬“爱国、进步、民主、科学”的五四精神,引领广大团员青年坚定理想信念,某市团委、少先队共同举办纪念“五四运动
周年,为进一步弘扬“爱国、进步、民主、科学”的五四精神,引领广大团员青年坚定理想信念,某市团委、少先队共同举办纪念“五四运动![]() 周年”读书演讲比赛,甲同学代表学校参加演讲比赛,
周年”读书演讲比赛,甲同学代表学校参加演讲比赛,![]() 位评委给该同学的打分(单位:分)情况如下表:
位评委给该同学的打分(单位:分)情况如下表:
评委 | 评委1 | 评委2 | 评委3 | 评委4 | 评委5 | 评委6 | 评委7 |
打分 |
|
|
|
|
|
|
|
(1)直接写出该同学所得分数的众数与中位数;
(2)计算该同学所得分数的平均数.