题目内容
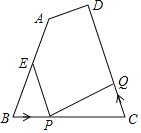
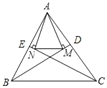
【题目】如图①,点![]() 是等边
是等边![]() 内一点,
内一点,![]() ,
,![]() .以
.以![]() 为边作等边三角形
为边作等边三角形![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
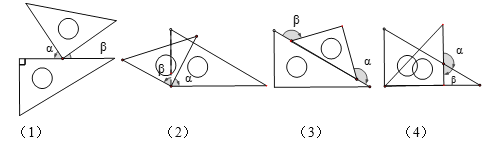
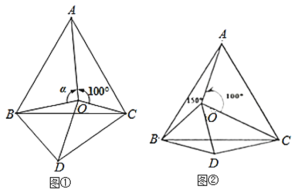
(2)当![]() 时(如图②),试判断
时(如图②),试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)求当![]() 是多少度时,
是多少度时,![]() 是等腰三角形?(写出过程)
是等腰三角形?(写出过程)
【答案】(1)证明见解析;
(2)![]() 是直角三角形,证明见解析;
是直角三角形,证明见解析;
(3)当![]() 为100°、130°、160°时,△AOD是等腰三角形.
为100°、130°、160°时,△AOD是等腰三角形.
【解析】
(1)利用等边三角形的性质证明![]() 即可;
即可;
(2)是直角三角形,利用![]() ,得到
,得到![]() ,再分别求出∠CDO、∠COD即可解答;
,再分别求出∠CDO、∠COD即可解答;
(3)分三种情况讨论:①![]() ②
②![]() ③
③![]() ,即可解答.
,即可解答.
(1)∵△ABC和△OBD是等边三角形
∴![]() 即
即![]()
在△ABO和△CBD中

∴![]()
(2)直角三角形
∵![]()
∴![]()
∵![]()
∴![]() ,
,![]()
∴△COD是直角三角形
(3)①![]() ,需
,需![]()
∴![]()
∴![]()
②![]() ,需
,需![]()
∴
∴![]()
③![]() ,需
,需![]()
∴![]()
∴![]()
∴当![]() 为100°、130°、160°时,△AOD是等腰三角形
为100°、130°、160°时,△AOD是等腰三角形

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
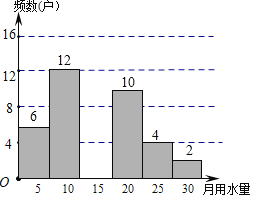
【题目】某校七(1)班学生为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,请解答以下问题;
级别 | A | B | C | D | E | F |
月均用水量x(t) | 0<x≤5 | 5<x≤10 | 10<x≤15 | 15<x≤20 | 20<x≤25 | 25<x≤30 |
频数(户) | 6 | 12 | m | 10 | 4 | 2 |
(1)本次调查采用的方式是 (填“全面调查”或“抽样调查);
(2)若将月均用水量的频数绘成形统计图,月均用水量“15<x≤20”组对应的圆心角度数是72°,则本次调查的样本容量是 ,表格中m的值是 ,补全频数分布直方图.
(3)该小区有500户家庭,求该小区月均用水量超过15t的家庭大约有多少户?