Question

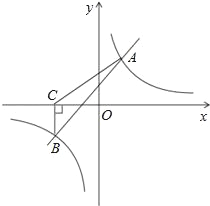
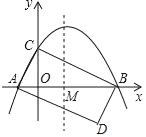
【题目】如图，抛物线y=ax2+bx+c与x轴交于点A（﹣1，0），B（4，0），与y轴交于点C（0，2）

(1)求抛物线的表达式；

(2)抛物线的对称轴与x轴交于点M，点D与点C关于点M对称，试问在该抛物线的对称轴上是否存在点P，使△BMP与△ABD相似？若存在，请求出所有满足条件的P点的坐标；若不存在，请说明理由．

Answer 1

【答案】(1)y=﹣x2+x+2；(2)满足条件的点P的坐标为（，）或（，﹣）或（，5）或（，﹣5）．

【解析】

（1）利用待定系数法求抛物线的表达式；

（2）使△BMP与△ABD相似的有三种情况，分别求出这三个点的坐标.

(1)∵抛物线与x轴交于点A（﹣1，0），B（4，0），

∴设抛物线的解析式为y=a（x+1）（x﹣4），

∵抛物线与y轴交于点C（0，2），

∴a×1×（﹣4）=2，

∴a=﹣，

∴抛物线的解析式为y=﹣（x+1）（x﹣4）=﹣x2+x+2；

(2)如图1，连接CD，∵抛物线的解析式为y=﹣x2+x+2，

∴抛物线的对称轴为直线x=，

∴M（，0），∵点D与点C关于点M对称，且C（0，2），

∴D（3，﹣2），

∵MA=MB，MC=MD，

∴四边形ACBD是平行四边形，

∵A（﹣1，0），B（4，0），C（3，﹣22），

∴AB2=25，BD2=（4﹣1）2+22=5，AD2=（3+1）2+22=20，

∴AD2+BD2=AB2，

∴△ABD是直角三角形，

∴∠ADB=90°，

设点P（，m），

∴MP=|m|，

∵M（，0），B（4，0），

∴BM=，

∵△BMP与△ABD相似，

∴①当△BMP∽ADB时，

∴，

∴，

∴m=±，

∴P（，）或（，﹣），

②当△BMP∽△BDA时，

，

∴，

∴m=±5，

∴P（，5）或（，﹣5），

即：满足条件的点P的坐标为P（，）或（，﹣）或（，5）或（，﹣5）．