题目内容
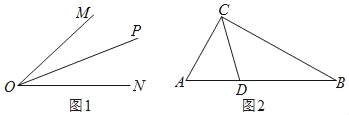
【题目】(解决问题)如图1,在![]() 中,
中,![]() ,
,![]() 于点
于点![]() .点
.点![]() 是
是![]() 边上任意一点,过点
边上任意一点,过点![]() 作
作![]() ,
,![]() ,垂足分别为点
,垂足分别为点![]() ,点
,点![]() .
.
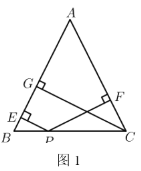
(1)若![]() ,
,![]() ,则
,则![]() 的面积是______,
的面积是______,![]() ______.
______.
(2)猜想线段![]() ,
,![]() ,
,![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
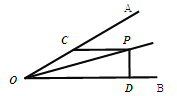
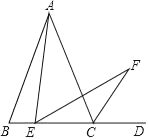
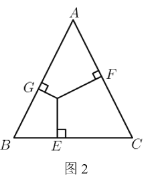
(3)(变式探究)如图2,在![]() 中,若
中,若![]() ,点
,点![]() 是
是![]() 内任意一点,且
内任意一点,且![]() ,
,![]() ,
,![]() ,垂足分别为点
,垂足分别为点![]() ,点
,点![]() ,点
,点![]() ,求
,求![]() 的值.
的值.
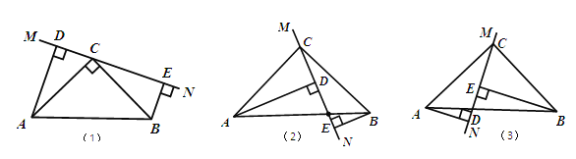
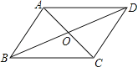
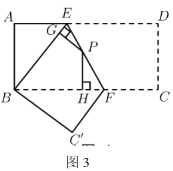
(4)(拓展延伸)如图3,将长方形![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 上,点
上,点![]() 落在点
落在点![]() 处,点
处,点![]() 为折痕
为折痕![]() 上的任意一点,过点
上的任意一点,过点![]() 作
作![]() ,
,![]() ,垂足分别为点
,垂足分别为点![]() ,点
,点![]() .若
.若![]() ,
,![]() ,直接写出
,直接写出![]() 的值.
的值.
【答案】(1)15,8;(2)![]() ,见解析;(3)
,见解析;(3)![]() ;(4)4
;(4)4
【解析】
解决问题(1)只需运用面积法:![]() ,即可解决问题;
,即可解决问题;
(2)解法同(1);
(3)连接![]() 、
、![]() 、
、![]() ,作
,作![]() 于
于![]() ,由等边三角形的性质得出
,由等边三角形的性质得出![]() ,由勾股定理得出
,由勾股定理得出![]() ,得出
,得出![]() 的面积
的面积![]() ,由
,由![]() 的面积
的面积![]() 的面积
的面积![]() 的面积
的面积![]() 的面积
的面积![]() ,即可得出答案;
,即可得出答案;
(4)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,易证
,易证![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,由解决问题(1)可得
,由解决问题(1)可得![]() ,易证
,易证![]() ,
,![]() ,只需求出
,只需求出![]() 即可.
即可.
解:(1)∵![]() ,
,![]() ,
,![]() ,
,
∴![]() 的面积
的面积![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
且![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
故答案为:15,8.
(2)∵![]() ,
,![]() ,
,![]() ,
,
且![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
(3)连接![]() 、
、![]() 、
、![]() ,作
,作![]() 于
于![]() ,如图2所示:
,如图2所示:
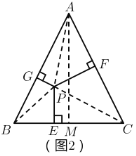
∵![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 的面积
的面积![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() 的面积
的面积![]() 的面积
的面积![]() 的面积
的面积![]() 的面积
的面积
![]()
![]()
![]() ,
,
∴![]() .
.
(4)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,如图3所示:
,如图3所示:
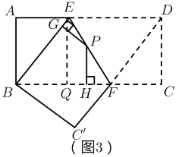
∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
由折叠可得:![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
由解决问题(1)可得:![]() ,
,
∴![]() ,即
,即![]() 的值为4.
的值为4.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目