题目内容
【题目】已知![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,点
,点![]() 是
是![]() 的中点,延长
的中点,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() (如图①).
(如图①).

(1)求证:![]() ≌
≌![]() ;
;
(2)已知点![]() 是
是![]() 的中点,连接
的中点,连接![]() (如图②).
(如图②).
①求证:![]() ≌
≌![]() ;
;
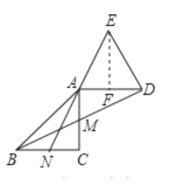
②如图③,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() ,求证:
,求证:![]() .
.
【答案】(1)见解析;(2)①见解析;②见解析.
【解析】
(1)由点M是AC中点知AM=CM,结合∠AMD=∠CMB和DM=BM即可得证;
(2)①由点M,N分别是AC,BC的中点及AC=BC可得CM=CN,结合∠C=∠C和BC=AC即可得证;
②过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,得∠NAC=∠AEF,由(1)可知
,得∠NAC=∠AEF,由(1)可知![]() ,
,![]() 则可证
则可证![]() ,可证
,可证![]() ≌
≌![]() ,据此知
,据此知![]() ,再证
,再证![]() ,又
,又![]() 得
得![]() ,又因为
,又因为![]() ,从而得
,从而得![]() ,即可得证.
,即可得证.
(1)∵![]() 是
是![]() 中点
中点
∴![]()
又∵![]()
![]()
∴在![]() 与
与![]() 中
中
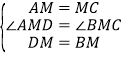
∴![]() ≌
≌![]() (
(![]() )
)
(2)① ![]()
![]() 是等腰直角三角形
是等腰直角三角形
∴ ![]()
∵ ![]() 是
是![]() 中点,
中点,![]() 是
是![]() 中点
中点
∴ ![]() ,
,![]()
∴ ![]()
又∵![]()
∴在![]() 与
与![]() 中
中

∴![]() ≌
≌![]() (
(![]() )
)
② 过点![]() 作
作![]() 交
交![]() 于点
于点![]()
∵ ![]()
∴ ![]()
由(1)可知![]() ≌
≌![]()
∴ ![]() ,
,![]()
∴ ![]()
∴ ![]()
在![]() 和
和![]() 中
中
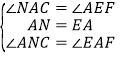
∴ ![]() ≌
≌![]() (
(![]() )
)
∴ ![]() ,
,![]() ,
,![]()
∵ ![]() 为
为![]() 中点
中点
∴ ![]() 为
为![]() 中点
中点
∴ ![]() 垂直平分
垂直平分![]()
∴ ![]()
∴ ![]()
∵ ![]()
∴ ![]()
∵ ![]()
∴ ![]()
即![]()
∴![]()

练习册系列答案
相关题目