Question

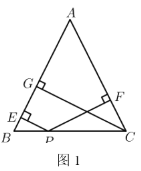
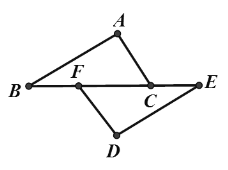
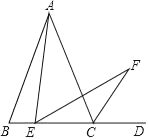
【题目】如图，在△ABC中，AB=AC=2，BC=4．点E为BC边上一动点，连接AE，作∠AEF=∠B，EF与△ABC的外角∠ACD的平分线交于点F．当EF⊥AC时，EF的长为_______．

Answer 1

【答案】1+

【解析】

当AB=AC，∠AEF=∠B时，∠AEF=∠ACB，当EF⊥AC时，∠ACB+∠CEF=90°=∠AEF+∠CEF，即可得到AE⊥BC，依据Rt△CFG≌Rt△CFH，可得CH=CG=，再根据勾股定理即可得到EF的长．

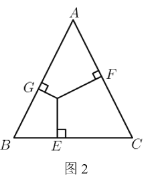
如图，

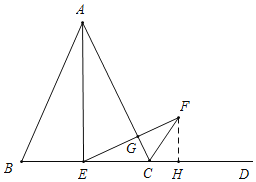
当AB=AC，∠AEF=∠B时，∠AEF=∠ACB，

当EF⊥AC时，∠ACB+∠CEF=90°=∠AEF+∠CEF，

∴AE⊥BC，

∴CE=BC=2，

又∵AC=2，

∴AE=4，EG==，

∴CG==，

作FH⊥CD于H，

∵CF平分∠ACD，

∴FG=FH，而CF=CF，

∴Rt△CFG≌Rt△CFH，

∴CH=CG=，

设EF=x，则HF=GF=x-，

∵Rt△EFH中，EH2+FH2=EF2，

∴（2+）2+（x-）2=x2，

解得x=1+，

故答案为：1+．