题目内容
【题目】如图，在平面直角坐标系
中，直线
（
）与直线
平行，且与直线
交于点
.
（1）求直线
的函数表达式；
（2）
、
分别是直线、
上两点，点的横坐标为
，且
轴，若
，求的值.
【答案】（1）
；（2）
的值是-1或3.
【解析】
（1）先利用直线
的解析式求出a的值，再根据直线
与直线
平行求出k的值，最后将点M的坐标代入的解析式可求出b的值，从而可得直线的函数表达式；
（2）由图可知，需分点D、E在点M的左侧和右侧两种情况分析，设点D、E的坐标，根据
建立等式求解即可.
（1）把
代入
得到
与直线平行
把
代入直线
中
得到
，解得
故直线的函数表达式为；
（2）因
轴，所以点D和点E的横坐标相同，
由直线和的解析式，可设
，
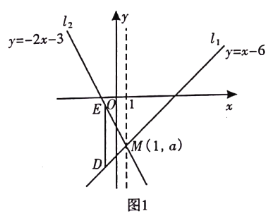
由图可知，需分点D、E在点M的左侧和右侧两种情况：
①如图1，当点D、E在点M的左侧，即
时，
∵，
∴
，
解得
；
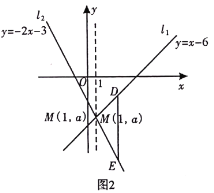
②如图2，当点D、E在点M的右侧，即
时，
∵，
∴
，
解得
，
综上所述，的值是-1或3.
练习册系列答案
名校课堂系列答案
相关题目
