题目内容
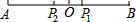 如图,已知线段AB,P1是AB的黄金分割点(AP1>BP1),点O是AB的中点,P2是P1关于点O的对称点.求证:P1B是P2B和P1P2的比例中项.
如图,已知线段AB,P1是AB的黄金分割点(AP1>BP1),点O是AB的中点,P2是P1关于点O的对称点.求证:P1B是P2B和P1P2的比例中项.考点:黄金分割
专题:证明题
分析:设AB=2,根据黄金分割的定义得AP1=
AB=
-1,则P1B=3-
,由点O是AB的中点得OB=1,所以OP1=
-2,由于P2是P1关于点O的对称点,则P1P2=2
-4,可计算出P2B=
-1,然后同过计算得到P1B2=14-6
,P2B•P1P2=14-6
,即P1B2=P2B•P1P2,所以P1B是P2B和P1P2的比例中项.
| ||
| 2 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
解答:证明:设AB=2,
∵P1是AB的黄金分割点(AP1>BP1),
∴AP1=
×2=
-1,
∴P1B=2-(
-1)=3-
,
∵点O是AB的中点,
∴OB=1,
∴OP1=1-(3-
)=
-2,
∵P2是P1关于点O的对称点,
∴P1P2=2(
-2)=2
-4,
∴P2B=2
-4+3-
=
-1,
∵P1B2=(3-
)2=14-6
,P2B•P1P2=(
-1)(2
-4)=14-6
,
∴P1B2=P2B•P1P2,
∴P1B是P2B和P1P2的比例中项.
∵P1是AB的黄金分割点(AP1>BP1),
∴AP1=
| ||
| 2 |
| 5 |
∴P1B=2-(
| 5 |
| 5 |
∵点O是AB的中点,
∴OB=1,
∴OP1=1-(3-
| 5 |
| 5 |
∵P2是P1关于点O的对称点,
∴P1P2=2(
| 5 |
| 5 |
∴P2B=2
| 5 |
| 5 |
| 5 |
∵P1B2=(3-
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
∴P1B2=P2B•P1P2,
∴P1B是P2B和P1P2的比例中项.
点评:本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点,其中AC=
AB≈0.618AB,并且线段AB的黄金分割点有两个.
| ||
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,等边△ABC内接于⊙O,点D为
如图,等边△ABC内接于⊙O,点D为
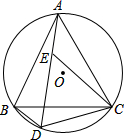
 如图,△ABC内接于⊙O,∠BAC的平分线分别交⊙O,BC于点D,E,连结BD.根据题意,找出图中各对相似三角形,并加以证明.
如图,△ABC内接于⊙O,∠BAC的平分线分别交⊙O,BC于点D,E,连结BD.根据题意,找出图中各对相似三角形,并加以证明.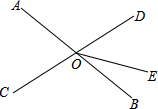 如图,直线AB,CD相交于O,已知∠AOC=75°,OE把∠BOD分成两部分,且∠BOE:∠EOD=2:3,求∠AOE.
如图,直线AB,CD相交于O,已知∠AOC=75°,OE把∠BOD分成两部分,且∠BOE:∠EOD=2:3,求∠AOE.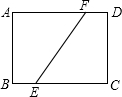 如图,已知矩形纸片ABCD的长为8,宽为6,把纸片对折,使点A与点C重合,求折痕EF的长.
如图,已知矩形纸片ABCD的长为8,宽为6,把纸片对折,使点A与点C重合,求折痕EF的长.
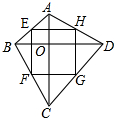 如图,四边形ABCD的对角线AC⊥BD,垂足为O,点E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是矩形.
如图,四边形ABCD的对角线AC⊥BD,垂足为O,点E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是矩形.