题目内容
7.已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.(1)如图①,求∠T和∠CDB的大小;
(2)如图②,当BE=BC时,求∠CDO的大小.
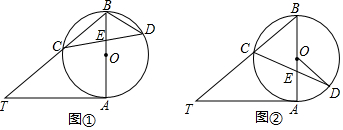
分析 (1)根据切线的性质:圆的切线垂直于经过切点的半径,得∠TAB=90°,根据三角形内角和得∠T的度数,由直径所对的圆周角是直角和同弧所对的圆周角相等得∠CDB的度数;
(2)如图②,连接AD,根据等边对等角得:∠BCE=∠BEC=65°,利用同圆的半径相等知:OA=OD,同理∠ODA=∠OAD=65°,由此可得结论.
解答  解:(1)如图①,连接AC,
解:(1)如图①,连接AC,
∵AT是⊙O切线,AB是⊙O的直径,
∴AT⊥AB,即∠TAB=90°,
∵∠ABT=50°,
∴∠T=90°-∠ABT=40°,
由AB是⊙O的直径,得∠ACB=90°,
∴∠CAB=90°-∠ABC=40°,
∴∠CDB=∠CAB=40°;
(2)如图②,连接AD,
在△BCE中,BE=BC,∠EBC=50°,
∴∠BCE=∠BEC=65°,
∴∠BAD=∠BCD=65°,
∵OA=OD,
∴∠ODA=∠OAD=65°,
∵∠ADC=∠ABC=50°,
∴∠CDO=∠ODA-∠ADC=65°-50°=15°.
点评 本题考查了圆的切线、圆周角定理、等腰三角形的性质、三角形的内角和,熟练掌握切线的性质是关键,注意运用同弧所对的圆周角相等.

练习册系列答案
相关题目
18. 如图,点A,B,C在⊙O上,∠AOB=72°,则∠ACB等于( )
如图,点A,B,C在⊙O上,∠AOB=72°,则∠ACB等于( )
 如图,点A,B,C在⊙O上,∠AOB=72°,则∠ACB等于( )
如图,点A,B,C在⊙O上,∠AOB=72°,则∠ACB等于( )| A. | 28° | B. | 54° | C. | 18° | D. | 36° |
15.据《天津日报》报道,天津市社会保障制度更加成熟完善,截止2017年4月末,累计发放社会保障卡12630000张.将12630000用科学记数法表示为( )
| A. | 0.1263×108 | B. | 1.263×107 | C. | 12.63×106 | D. | 126.3×105 |
12.下列选项中的整数,与$\sqrt{17}$最接近的是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
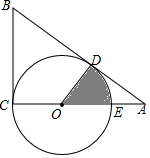 如图,O为Rt△ABC的直角边AC上一点,以 OC为半径的⊙O与斜边AB相切于点D,交OA于点E.已知BC=$\sqrt{3}$,AC=3.
如图,O为Rt△ABC的直角边AC上一点,以 OC为半径的⊙O与斜边AB相切于点D,交OA于点E.已知BC=$\sqrt{3}$,AC=3.