题目内容
在平面直角坐标系中, 抛物线
 +
+ 与直线
与直线 交于A, B两点,点A在点B的左侧.
交于A, B两点,点A在点B的左侧.
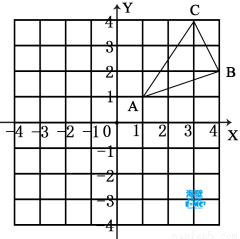
(1)如图1,当 时,直接写出A,B两点的坐标;
时,直接写出A,B两点的坐标;
(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
(3)如图2,抛物线
 +
+ 
 与
与 轴交于C,D两点(点C在点D的左侧).在直线
轴交于C,D两点(点C在点D的左侧).在直线 上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时
上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

图1 图2
(1)A(-1,0) ,B(2,3)
(2)△ABP最大面积s=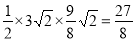 ; P(
; P(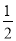 ,-
,-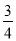 )
)
(3)存在;k=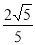
【解析】
试题分析:(1)将两个解析式联立组成方程组,解方程组即得
要想△ABP的面积最大,则要在要求的抛物线上找到一个点P,使点P到直线AB的距离最大,这时过点P且与AB平行的直线与抛物线只有一个交点,利用根的判别式可确定平移后所得直线的解析式,进而可得点的坐标,求出面积
设圆心为E,连接EQ,直线与x轴交点为H,与y轴交点为F;由已知可得直线与两坐标轴交点的坐标,从而可得直线与坐标轴交点到原点的距离;由圆的切线及相似的知识可得出EQ、QH的长,
再由勾股定理可得要求的值
试题解析:(1)A(-1,0) ,B(2,3)
(2)平移直线AB得到直线L,当L与抛物线只有一个交点时,△ABP面积最大[如图12-1(1)]

设直线L解析式为: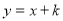 ,
,
根据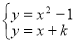 ,得
,得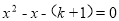
判别式△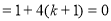 ,解得,
,解得,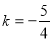
代入原方程中,得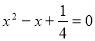 ;解得,
;解得,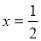 ,
, 
∴P(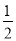 ,
,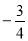 )
)
易求,AB交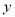 轴于M(0,1),直线L交轴
轴于M(0,1),直线L交轴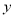 于G(0,
于G(0,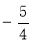 )
)
过M作MN⊥直线L于N,∵OM=1,OA=1,∴∠AMO=45°
∵∠AMN=90,∴∠NMO=45°
在RT△MNE中,∠NMO=45°,MG=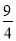 ,[如图12-1(2)]
,[如图12-1(2)]
∴ MN=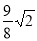 ,MN即为△ABP的高
,MN即为△ABP的高
由两点间距离公式,求得:AB=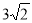
故△ABP最大面积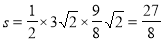
(3)设在直线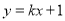 上存在唯一一点Q使得∠OQC=90°
上存在唯一一点Q使得∠OQC=90°
则点Q为以OC的中点E为圆心,OC为直径形成的圆E与直线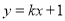 相切时的切点,[如图12-2(1)]
相切时的切点,[如图12-2(1)]
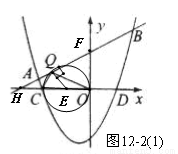
由解析式可知:C(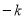 ,0),OC=
,0),OC=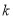 ,则圆E的半径:OE=CE=
,则圆E的半径:OE=CE=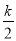 =QE
=QE
设直线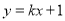 与
与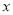 、
、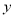 轴交于H点和F点,则F(0,1),∴OF=1 则H(
轴交于H点和F点,则F(0,1),∴OF=1 则H(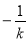 ,0), ∴OH =
,0), ∴OH =
∴ EH=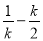
∵AB为切线 ∴EQ⊥AB,∠EQH=90°
在△FOH和△EQH中 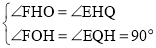
∴△FOH∽△EQH
∴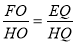 ∴ 1:
∴ 1: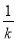 =
=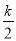 :QH,∴QH =
:QH,∴QH =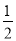
在RT△EQH中,EH=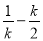 ,QH =
,QH =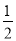 ,QE =
,QE =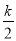 ,根据勾股定理得,
,根据勾股定理得,
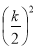 +
+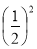 =
=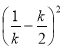
求得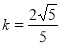
考点:1、平面直角坐标系中的平行与垂直;2、二次函数;3、一元二次方程根的判别式;4、圆(相切、圆心角)