题目内容
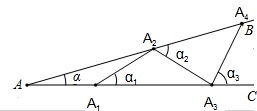 如图,设∠BAC=α(0°<α<90°).用一些等长的小木棒,从点A1开始,向右依次摆放在两射线之间,并使小木棒的两端恰好分别落在射线AB、AC上,其中A1A2为第一根小木棒,且AA1=A1A2.
如图,设∠BAC=α(0°<α<90°).用一些等长的小木棒,从点A1开始,向右依次摆放在两射线之间,并使小木棒的两端恰好分别落在射线AB、AC上,其中A1A2为第一根小木棒,且AA1=A1A2.
(1)若已经摆放了3根小木棒,则α2=______(用含α的式子表示).
(2)若只能摆放4根小木棒,则α的取值范围是______.
 解:(1)∵小木棒长度都相等,
解:(1)∵小木棒长度都相等,∴∠1=∠α,∠2=∠α1,
由三角形外角性质,∠α1=∠1+∠α=2∠α,
∠α2=∠α+∠α1=∠α+2∠α=3α;
(2)依此类推,∠α3=4α,∠α4=5α,
∵只能摆放4根小木棒,
∴
 ,
,解得18°≤α<22.5°.
故答案为:3α;18°≤α<22.5°.
分析:(1)根据等边对等角可得∠1=∠α,∠2=∠α1,再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解;
(2)求出第三根小木棒构成的三角形,然后三角形的内角和定理和外角性质列出不等式组求解即可.
点评:本题考查了等腰三角形等边对等角的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,三角形的内角和定理,(2)列出不等式组是解题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目

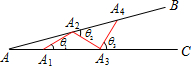 如图,设∠BAC=θ(0°<θ<90°).现把小棒依次摆放在两射线之间,并使小棒两端分别落在射线AB,AC上.从点A1开始,用等长的小棒依次向右摆放,其中A1A2为第一根小棒,且A1A2=AA1.
如图,设∠BAC=θ(0°<θ<90°).现把小棒依次摆放在两射线之间,并使小棒两端分别落在射线AB,AC上.从点A1开始,用等长的小棒依次向右摆放,其中A1A2为第一根小棒,且A1A2=AA1. 如图,设∠BAC=α(0°<α<90°).用一些等长的小木棒,从点A1开始,向右依次摆放在两射线之间,并使小木棒的两端恰好分别落在射线AB、AC上,其中A1A2为第一根小木棒,且AA1=A1A2.
如图,设∠BAC=α(0°<α<90°).用一些等长的小木棒,从点A1开始,向右依次摆放在两射线之间,并使小木棒的两端恰好分别落在射线AB、AC上,其中A1A2为第一根小木棒,且AA1=A1A2.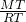 为定值.上述结论有且只有一个是正确的,请选择你认为正确的结论度证明求值.
为定值.上述结论有且只有一个是正确的,请选择你认为正确的结论度证明求值.