题目内容
(1)(5- )2
)2
(2)
(3)( -2)2004×(
-2)2004×( +2)2003
+2)2003
(4) +(1-
+(1- )0
)0
解:(1)原式=25-10 +7
+7
=32-10 ;
;
(2)原式=2 +4
+4 -
-
=5 ;
;
(3)原式=[( -2)(
-2)( +2)]2003(
+2)]2003( -2)
-2)
=(5-4)2003( -2)
-2)
= -2;
-2;
(4)原式= +1
+1
= +1
+1
=5+1
=6.
分析:(1)利用完全平方公式进行计算;
(2)先把各二次根式化为最简二次根式得到原式=2 +4
+4 -
- ,然后合并同类二次根式;
,然后合并同类二次根式;
(3)根据积的乘方得到原式=[( -2)(
-2)( +2)]2003(
+2)]2003( -2),然后利用平方差公式进行计算;
-2),然后利用平方差公式进行计算;
(4)根据零指数幂和把各二次根式化为最简二次根式得到原式= +1,再把分子合并后进行二次根式的除法运算.
+1,再把分子合并后进行二次根式的除法运算.
点评:本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.
 +7
+7=32-10
 ;
;(2)原式=2
 +4
+4 -
-
=5
 ;
;(3)原式=[(
 -2)(
-2)( +2)]2003(
+2)]2003( -2)
-2)=(5-4)2003(
 -2)
-2)=
 -2;
-2;(4)原式=
 +1
+1=
 +1
+1=5+1
=6.
分析:(1)利用完全平方公式进行计算;
(2)先把各二次根式化为最简二次根式得到原式=2
 +4
+4 -
- ,然后合并同类二次根式;
,然后合并同类二次根式;(3)根据积的乘方得到原式=[(
 -2)(
-2)( +2)]2003(
+2)]2003( -2),然后利用平方差公式进行计算;
-2),然后利用平方差公式进行计算;(4)根据零指数幂和把各二次根式化为最简二次根式得到原式=
 +1,再把分子合并后进行二次根式的除法运算.
+1,再把分子合并后进行二次根式的除法运算.点评:本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
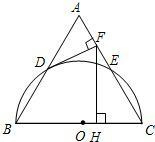 C,垂足为点F.
C,垂足为点F. ,
, 两个数(如图1);第二次又在第一次标出的两个之间的圆周上,分别标出这两个数的和(如图2);第三次再在第二次标出的所有相邻两数之间的圆周上,分别标出相邻两数的和(如图3);按此规则,依此类推,一直标下去.
两个数(如图1);第二次又在第一次标出的两个之间的圆周上,分别标出这两个数的和(如图2);第三次再在第二次标出的所有相邻两数之间的圆周上,分别标出相邻两数的和(如图3);按此规则,依此类推,一直标下去.
 等腰△ABC中,AB=AC,E、F分别在AB、AC上,AE=AF,试证明四边形EBCF是等腰梯形.
等腰△ABC中,AB=AC,E、F分别在AB、AC上,AE=AF,试证明四边形EBCF是等腰梯形. a3b+a2b2+
a3b+a2b2+ ,
, .
. ,-7,2.5,π,
,-7,2.5,π, 的上方作正方形BEFG,为DC与EF的交点,请探索:
的上方作正方形BEFG,为DC与EF的交点,请探索: 已知:如图,AB、CD是⊙O的两条弦,AB=CD.
已知:如图,AB、CD是⊙O的两条弦,AB=CD.