Question

11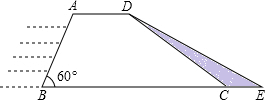．水利部门决定对某水库大坝进行加固，大坝的横截面是梯形ABCD．如图所示，已知迎水坡面AB的长为4米，∠B=60°，背水坡面CD的长为4$\sqrt{3}$米，加固后大坝的横截面积为梯形ABED，CE的长为2米．
（1）已知需加固的大坝长为150米，求需要填土石方多少立方米？
（2）求加固后的大坝背水坡DE的坡度．

Answer 1

分析 （1）分别过A、D作下底的垂线，设垂足为F、G．在Rt△ABF中，已知坡面长和坡角的度数，可求得铅直高度AF的值，也就得到了DG的长；以CE为底，DG为高即可求出△CED的面积，再乘以大坝的长度，即为所需的填方体积；
（2）在Rt△CDG中，由勾股定理求CG的长，即可得到GE的长；Rt△DEG中，根据DG、GE的长即可求得坡角的正切值，即坡面DE的坡比．

解答 解：（1）分别过A、D作AF⊥BC，DG⊥BC，垂点分别为F、G，如图所示．
∵在Rt△ABF中，AB=4米，∠B=60°，
sinB=$\frac{AF}{AB}$，
∴在矩形AFGD中，AF=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$（米），DG=AF=2 $\sqrt{3}$米
∴S_△DCE=$\frac{1}{2}$×CE×DG=$\frac{1}{2}$×2×2 $\sqrt{3}$=2$\sqrt{3}$（平方米）
需要填方：150×2$\sqrt{3}$=300$\sqrt{3}$（立方米）；

（2）在直角三角形DGC中，DC=4$\sqrt{3}$米，
∴GC=$\sqrt{C{D}^{2}-D{G}^{2}}$=6米，
∴GE=GC+CE=8米，
坡度i=DG：GE=2$\sqrt{3}$：8=$\sqrt{3}$：4．

点评 此题主要考查学生对坡度坡角的掌握及三角函数的运用能力．解题的关键是牢记坡度是竖直高度与水平宽度的比值．