Question

9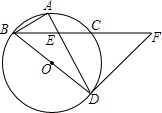．如图，BD为⊙O的直径，点A是弧BC的中点，AD交BC于E点，AE=2，ED=4．
（1）求证：△ABE∽△ADB；
（2）求tan∠ADB的值；
（3）延长BC至F，连接FD，使△BDF的面积等于8$\sqrt{3}$，求∠F的度数．

Answer 1

分析 （1）由于A是弧BC的中点，故∠ADB=∠ABC，再加上公共角∠A，即可证得所求的三角形相似．
（2）由（1）的相似三角形所得比例线段，可求得AB的长，进而可在Rt△ABD中，求得∠ABD的正切值．
（3）连接CD，由（2）知∠ADB=30°，那么∠CDE=30°，∠CED=60°，由DE的长即可得到CD的值，进而可由△BDF的面积求得BF的长，进而可求得EF=ED=4，由此可证得△EDF是正三角形，即可得∠F的度数．

解答 （1）证明：∵点A是弧BC的中点，
∴∠ABC=∠ADB，
又∵∠BAE=∠BAE，
∴△ABE∽△ADB；

（2）解：∵△ABE∽△ADB，
∴AB²=2×6=12，
∴AB=2$\sqrt{3}$，
在Rt△ADB中，tan∠ADB=$\frac{2\sqrt{3}}{8}$；

（3）解：连接CD，则∠BCD=90°；
由（2）得：∠ADB=∠EDC=30°，∠CED=60°；
已知DE=4，则CD=2$\sqrt{3}$；
∵S_△BDF=$\frac{1}{2}$×BF×2$\sqrt{3}$=8$\sqrt{3}$，即BF=8；
易得∠EBD=∠EDB=30°，即BE=DE=4，
∴EF=DE=4，又∠CED=60°，
∴△DEF是正三角形，
故∠F=60°．

点评 此题主要考查了相似三角形的判定和性质、圆周角定理、圆心角、弧的关系、等边三角形的判定和性质等知识，熟练应用相似三角形的判定与性质是解题关键．