题目内容
【题目】已知函数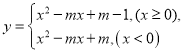 将此函数的图象记为
将此函数的图象记为![]() .
.
(1)当![]() 时,
时,
![]() 直接写出此函数的函数表达式.
直接写出此函数的函数表达式.
![]() 点
点![]() 在图象
在图象![]() 上,求点
上,求点![]() 的坐标.
的坐标.
![]() 点
点![]() 在图象
在图象![]() 上,求
上,求![]() 的值.
的值.
(2)设图象![]() 最低点的纵坐标为
最低点的纵坐标为![]() .当
.当![]() 时,直接写出
时,直接写出![]() 的值.
的值.
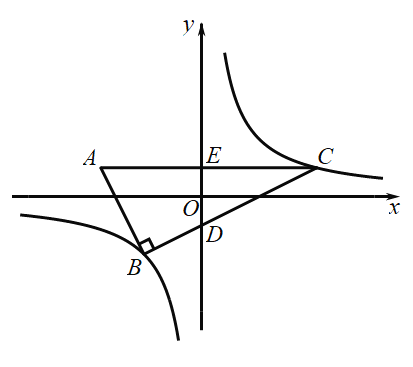
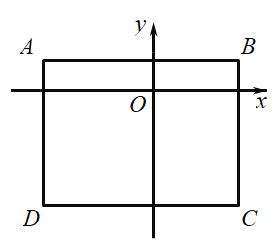
(3)矩形![]() 的顶点坐标分别为
的顶点坐标分别为![]() 若函数
若函数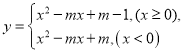 在
在![]() 范围内的图象与矩形
范围内的图象与矩形![]() 的边有且只有一个公共点,直接写出此时
的边有且只有一个公共点,直接写出此时![]() 的取值范围.
的取值范围.
【答案】(1)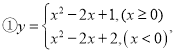 ②
②![]() ;③
;③![]() 或
或![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() 或
或![]() 或
或![]()
【解析】
(1)①把![]() 代入函数表达式
代入函数表达式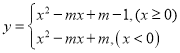 整理即可;
整理即可;
②由点![]() 在函数图象
在函数图象![]() 上,因为-1<0,所以把
上,因为-1<0,所以把![]() 代入
代入![]() ,即可求出P点坐标;
,即可求出P点坐标;
③当![]() 时,把
时,把![]() 代入
代入![]() ,即可求出b的值;
,即可求出b的值;
当当![]() 时,把
时,把![]() 代入
代入![]() ,即可计算出b的值;
,即可计算出b的值;
(2)因为图象![]() 最低点的纵坐标为
最低点的纵坐标为![]() ,需分两种进行讨论:当在抛物顶点上取得最小值时所以把
,需分两种进行讨论:当在抛物顶点上取得最小值时所以把![]() 代入函数表达式得
代入函数表达式得![]() ,形成一个一元二次方程,让判别式△=0,即可求出符合题意的m的值;当函数G的最大值在y轴上取得时,
,形成一个一元二次方程,让判别式△=0,即可求出符合题意的m的值;当函数G的最大值在y轴上取得时,![]() ,此时m = -1.
,此时m = -1.
(3) 需分情况讨论分析.具体要探x取值全在在y轴右侧时,函数![]() 与矩形
与矩形![]() 只有一个公共点时,当
只有一个公共点时,当![]() ,即
,即![]() 时;x取值全在在y轴右侧时,函数
时;x取值全在在y轴右侧时,函数![]() 与矩形
与矩形![]() 只有一个公共点时,
只有一个公共点时,![]() ;另外不要忘记还有一个孤点,当
;另外不要忘记还有一个孤点,当![]() 时,函数G的图像也只有一个公共点.
时,函数G的图像也只有一个公共点.
解:(1)①根据题意把![]() 代入函数表达式
代入函数表达式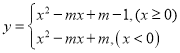 整理即可得:
整理即可得: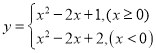 ;
;
![]() 当
当![]() 时,把
时,把![]() 代入
代入![]() 得
得
![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
![]() 当
当![]() 时,把
时,把![]() 代入
代入![]() 得:
得:
![]()
解得![]() (舍).
(舍).
当![]() 时,
时,![]() 代入
代入![]() 得:
得:
![]()
解得![]() (舍),
(舍),![]() .
.
![]() 的值为
的值为![]() 或
或![]() .
.
(2)当![]() 符合题意时
符合题意时
∴![]()
∴![]() =0
=0
∴![]()
解得![]() ,
, ![]() (舍去)
(舍去)
当x=0,函数G取得最小值时
![]()
∴m = -1
综上所述,![]() 的值为
的值为![]() 或
或![]() .
.
(3)根据题意得,要使函数G与矩形![]() 有公共点,
有公共点,
则-4≤x≤3,-4≤y≤1
∵![]()
当![]() ,即
,即![]() 时
时
此时函数![]() 与矩形
与矩形![]() 只有一个公共点
只有一个公共点
当![]() ,即
,即![]() 时
时
要使函数![]() 与矩形
与矩形![]() 只有一个公共点,
只有一个公共点,
则![]()
另外,当![]() 时,函数G与矩形
时,函数G与矩形![]() 也只有一个公共点
也只有一个公共点
综上所述,函数G与矩形![]() 只有一个公共点的符合条件的m的取值范围是:
只有一个公共点的符合条件的m的取值范围是:![]() 或
或![]() 或
或![]()

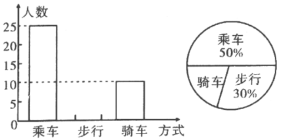
【题目】现在,步行运动深受广大健身爱好者的喜爱. 通过“微信运动”可以查询微信好友当天的行走步数.实验中学张老师根据该校![]() 名教师某日“微信运动”中的行走步数,绘制成如下两张统计表(不完整).
名教师某日“微信运动”中的行走步数,绘制成如下两张统计表(不完整).
步数 | 频数 | 频率 |
|
| 0.2 |
| 19 | 0.38 |
|
| 0.3 |
| 4 |
|
| 2 | 0.04 |
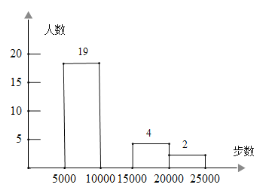
(1)写出左表中![]() 、
、![]() 、
、![]() 的值,并补全条形统计图;
的值,并补全条形统计图;
(2)实验中学所在的某县有![]() 名教师,用张老师调查的样本数据估计该县当天行走步数不少于
名教师,用张老师调查的样本数据估计该县当天行走步数不少于![]() 步的教师有多少人?
步的教师有多少人?
(3)在该校![]() 名教师中,随机选取当天行走步数不少于
名教师中,随机选取当天行走步数不少于![]() 步的
步的![]() 名教师参加“我运动,我健康”的征文活动,求选中的
名教师参加“我运动,我健康”的征文活动,求选中的![]() 名教师的行走步数都不小于
名教师的行走步数都不小于![]() 步的概率.
步的概率.
【题目】李辉到服装专卖店去做社会调查,了解到商店为了激励营业员的工作积极性实行了“月总收入=基本工资+计件奖金”的方法,并获得了如下信息:
营业员 | 嘉琪 | 嘉善 |
月销售件数/件 | 400 | 300 |
月总收入/元 | 7800 | 6600 |
假设月销售件数为x件,月总收入为y元,销售每件奖励a元,营业员月基本工资为b元.
(1)求a、b的值.
(2)若营业员嘉善某月总收入不低于4200元,那么嘉善当月至少要卖多少件衣服?