题目内容
15.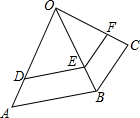 如图,DE∥AB,$\frac{OA}{OD}$=$\frac{OC}{OF}$,求证:EF∥BC.
如图,DE∥AB,$\frac{OA}{OD}$=$\frac{OC}{OF}$,求证:EF∥BC.
分析 根据平行线分线段成比例定理求出$\frac{OA}{OD}$=$\frac{OB}{OE}$,求出$\frac{OC}{OF}$=$\frac{OB}{OE}$,根据相似三角形的判定定理推出△OEF∽△OBC,根据相似三角形的性质得出∠OEF=∠OBC即可.
解答 证明:∵DE∥AB,
∴$\frac{OA}{OD}$=$\frac{OB}{OE}$,
∵$\frac{OA}{OD}$=$\frac{OC}{OF}$,
∴$\frac{OC}{OF}$=$\frac{OB}{OE}$,
∵∠EOF=∠BOC,
∴△OEF∽△OBC,
∴∠OEF=∠OBC,
∴EF∥BC.
点评 本题考查了平行线的判定,相似三角形的性质和判定,平行线分线段成比例定理的应用,能推出△OEF∽△OBC是解此题的关键.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
6.计算22+22+22+22的结果是( )
| A. | 23 | B. | 82 | C. | 24 | D. | 28 |
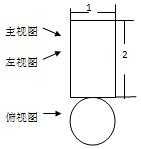 如图,长方形是一个几何体从正面看和从左面看到的形状图,圆是从上面看到的形状图(含有数据),则这个几何体的侧面展开图的面积等于( )
如图,长方形是一个几何体从正面看和从左面看到的形状图,圆是从上面看到的形状图(含有数据),则这个几何体的侧面展开图的面积等于( )