题目内容
15. 如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠ABC=60°,∠C=70°,求∠DAC,∠BOA,∠EAD的度数.
如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠ABC=60°,∠C=70°,求∠DAC,∠BOA,∠EAD的度数.
分析 根据三角形内角和定理、三角形的高的定义、角平分线的定义计算即可.
解答 解:∵AD是高,
∴∠ADC=90°,
∵∠C=70°,
∴∠DAC=90°-∠C=90°-70°=20°,
∵∠ABC+∠C+∠BAC=180°,
∴∠BAC=180°-(∠ABC+∠C)=180°-(60°+70°)=50°,
∵AE、BF是角平分线,
∴∠ABF=$\frac{1}{2}$∠ABC=$\frac{1}{2}$×60°=30°,∠BAE=∠EAC=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×50°=25°,
∴∠BOA=180°-(∠1+∠2)=180°-(30°+25°)=125°,
∠EAD=∠EAC-∠DAC=25°-20°=5°.
点评 本题考查的是三角形内角和定理、三角形的高、角平分线的定义,掌握三角形内角和等于180°是解题的关键.

练习册系列答案
相关题目
20.用代数式表示:“x的5倍与y的和的一半”可以表示为( )
| A. | 5x+$\frac{1}{2}$y | B. | $\frac{1}{2}$(5x+y) | C. | (5x+y)$\frac{1}{2}$ | D. | 5x+y |
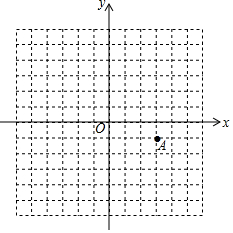 如图,在网格中有点A(3,-1).
如图,在网格中有点A(3,-1).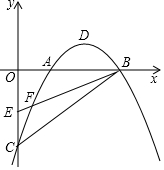 已知:如图,在平面直角坐标系中,已知抛物线y=ax2+bx-2(a≠0)与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C,其顶点为点D,点E的坐标为(0,-1),该抛物线与BE交于另一点F,连接BC.
已知:如图,在平面直角坐标系中,已知抛物线y=ax2+bx-2(a≠0)与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C,其顶点为点D,点E的坐标为(0,-1),该抛物线与BE交于另一点F,连接BC. 已知抛物线y=-x2+4x+5与x轴的交点A,B(A在B的左边),顶点为P.
已知抛物线y=-x2+4x+5与x轴的交点A,B(A在B的左边),顶点为P.