题目内容
 已知,AD为△ABC(AB>AC)的角平分线,AD的垂直平分线和BC的延长线交于点E,设CE=a,DE=b,BE=c.求证:关于x的二次方程ax2-2bx+c=0有两个相等的实根.
已知,AD为△ABC(AB>AC)的角平分线,AD的垂直平分线和BC的延长线交于点E,设CE=a,DE=b,BE=c.求证:关于x的二次方程ax2-2bx+c=0有两个相等的实根.
 解:连接EA,如下图所示:
解:连接EA,如下图所示:∵EF垂直平分AD,
∴EA=ED,∠EAD=∠EDA.
即∠EAC+∠CAD=∠B+∠BAD.
又∠CAD=∠BAD.
故∠EAC=∠B;又∠AEC=∠BEA.
∴△ABE∽△CAE.
∴AE2=CE•BE,
∵设CE=a,DE=b,BE=c.
∴b2=a•c,
∴b2-a•c=0,
∵ax2-2bx+c=0,
△=(2b)2-4ac=4(b2-a•c)=0,
∴关于x的二次方程ax2-2bx+c=0有两个相等的实根.
分析:连接EA,由已知中AD为∠BAC的平分线,AD的垂直平分线EF与AD交于点F,与BC的延长线交于点E,可证得△ABE∽△CAE,由相似三角形的性质,可得AE2=CE•BE,再利用根与系数关系,即可得到答案.
点评:此题考查了相似三角形的性质以及根与系数的关系,根据已知得出△ABE∽△CAE是解答本题的关键.

练习册系列答案
相关题目
 认真阅读,并回答下面问题:
认真阅读,并回答下面问题:

 阅读并解答问题.
阅读并解答问题. 已知:AD为△ABC的中线,AE是△ABD的中线,AB=BD.
已知:AD为△ABC的中线,AE是△ABD的中线,AB=BD.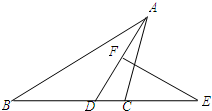 已知,AD为△ABC(AB>AC)的角平分线,AD的垂直平分线和BC的延长线交于点E,设CE=a,DE=b,BE=c.求证:关于x的二次方程ax2-2bx+c=0有两个相等的实根.
已知,AD为△ABC(AB>AC)的角平分线,AD的垂直平分线和BC的延长线交于点E,设CE=a,DE=b,BE=c.求证:关于x的二次方程ax2-2bx+c=0有两个相等的实根.