题目内容
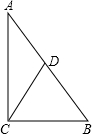
 已知:AD为△ABC的中线,AE是△ABD的中线,AB=BD.
已知:AD为△ABC的中线,AE是△ABD的中线,AB=BD.(1)判断△ABE与△CBA是否相似并说明理由;
(2)求证:AC=2AE.
分析:(1)根据“两边及其夹角法(两组对应边的比相等且夹角对应相等的两个三角形相似)推知△ABE与△CBA相似;
(2)利用(1)中相似三角形的对应边成比例证明该结论.
(2)利用(1)中相似三角形的对应边成比例证明该结论.
解答: (1)解:∵AD为△ABC的中线,AE是△ABD的中线,
(1)解:∵AD为△ABC的中线,AE是△ABD的中线,
∴BD=CD,BE=DE,
∴BE=
BD,BD=
BC;
又∵AB=BD,
∴BE=
AB,AB=
BC,
∴
=
=
,∠B=∠B,
∴△ABE∽△CBA;
(2)证明:∵由(1)知,△ABE∽△CBA,
∴
=
=
,
∴AC=2AE.
 (1)解:∵AD为△ABC的中线,AE是△ABD的中线,
(1)解:∵AD为△ABC的中线,AE是△ABD的中线,∴BD=CD,BE=DE,
∴BE=
| 1 |
| 2 |
| 1 |
| 2 |
又∵AB=BD,
∴BE=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| BE |
| AB |
| AB |
| BC |
| 1 |
| 2 |
∴△ABE∽△CBA;
(2)证明:∵由(1)知,△ABE∽△CBA,
∴
| AE |
| AC |
| BE |
| AB |
| 1 |
| 2 |
∴AC=2AE.
点评:本题考查了相似三角形的判定与性质.相似三角形相似多边形的特殊情形,它沿袭相似多边形的定义,从对应边的比相等和对应角相等两方面下定义;反过来,两个三角形相似也有对应角相等,对应边的比相等.

练习册系列答案
相关题目
 认真阅读,并回答下面问题:
认真阅读,并回答下面问题:

 阅读并解答问题.
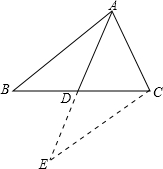
阅读并解答问题.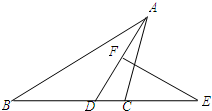 已知,AD为△ABC(AB>AC)的角平分线,AD的垂直平分线和BC的延长线交于点E,设CE=a,DE=b,BE=c.求证:关于x的二次方程ax2-2bx+c=0有两个相等的实根.
已知,AD为△ABC(AB>AC)的角平分线,AD的垂直平分线和BC的延长线交于点E,设CE=a,DE=b,BE=c.求证:关于x的二次方程ax2-2bx+c=0有两个相等的实根.