Question

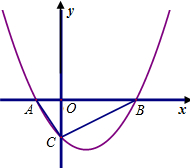
如图，将抛物线y=x²沿x轴正方向平移3个单位得到抛物线l，直线y=-2．
（1）求抛物线l的解析式；
（2）点A是抛物线l上一点，点B是直线y=-2上一点，是否存在等腰△OAB？若存在，求点A，B两点的坐标；若不存在，说明理由；
（3）若将上题中的“沿x轴正方向平移3个单位”改为“沿x轴正方向平移n个单位”，其它条件不变，探究上题（2）中的问题．

Answer 1

（1）抛物线y=x²沿x轴正方向平移3个单位得到抛物线l的解析式为y=（x-3）²；

（2）存在，当OA=OB时，即AB关于x轴对称时，三角形OAB为的等腰三角形，
设B点坐标为（x，-2）则A点坐标为A（x，2），
又∵点A是抛物线l上一点，
∴（x-3）²=2，解得x=3+

2

或x=3-

2

，
∴AB两点的坐标分别为A（3+

2

，2），B（3+

2

，-2）或为A（3-

2

，2），B（3-

2

，-2）；

（3）抛物线y=x²沿x轴正方向平移n个单位得到抛物线l的解析式为y=（x-n）²；
若三角形OAB为的等腰三角形，则OA=OB，即AB关于x轴对称，
设B点坐标为（x，-2）则A点坐标为A（x，2），
又∵点A是抛物线l上一点，
∴（x-n）²=2，解得x=n+

2

或x=n-

2

，
∴AB两点的坐标分别为A（n+

2

，2），B（n+

2

，-2）或为A（n-

2

，2），B（n-

2

，-2）；