Question

12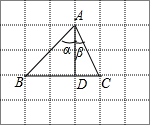．△ABC在网格中的位置如图所示（每个小正方形边长为1），AD⊥BC于D，下列四个选项中，错误的是（　　）

• A． sinα=cosα
• B． tanC=2
• C． sinβ=cosβ
• D． tanα=1

Answer 1

分析 观察图象可知，△ADB是等腰直角三角形，BD=AD=2，AB=2$\sqrt{2}$，AD=2，CD=1，AC=$\sqrt{5}$，利用锐角三角函数一一计算即可判断．

解答 解：观察图象可知，△ADB是等腰直角三角形，BD=AD=2，AB=2$\sqrt{2}$，AD=2，CD=1，AC=$\sqrt{5}$，
∴sinα=cosα=$\frac{\sqrt{2}}{2}$，故A正确，
tanC=$\frac{AD}{CD}$=2，故B正确，
tanα=1，故D正确，
③∵sinβ=$\frac{CD}{AC}$=$\frac{\sqrt{5}}{5}$，cosβ=$\frac{2\sqrt{5}}{5}$，
∴sinβ≠cosβ，故C错误．
故选C．

点评 本题考查锐角三角函数的应用．等腰直角三角形的判定和性质、勾股定理等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．