题目内容
16.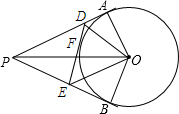 如图,∠APB=52°,PA、PB、DE都为⊙O的切线,切点分别为A、B、F,且PA=6.
如图,∠APB=52°,PA、PB、DE都为⊙O的切线,切点分别为A、B、F,且PA=6.(1)求△PDE的周长;
(2)求∠DOE的度数.
分析 (1)根据切线长定理得到DA=DF,EB=EF,PA=PB=6,于是得到DE=DA+EB,即可得到结论;
(2)根据切线的性质得到OB⊥PB,OA⊥PA,∠BOE=∠FOD=$\frac{1}{2}$∠BOF,∠FOD=∠AOD=$\frac{1}{2}$∠AOF,根据四边形的内角和得到∠AOB=360°-90°-90°-52°=128°,即可得到结论.
解答  解:(1)∵PA、PB、DE都为⊙O的切线,
解:(1)∵PA、PB、DE都为⊙O的切线,
∴DA=DF,EB=EF,PA=PB=6,
∴DE=DA+EB,
∴PE+PD+DE=PA+PB=12,
即△PDE的周长为12;
(2)连接OF,
∵PA、PB、DE分别切⊙O于A、B、F三点,
∴OB⊥PB,OA⊥PA,∠BOE=∠FOD=$\frac{1}{2}$∠BOF,∠FOD=∠AOD=$\frac{1}{2}$∠AOF,
∵∠APB=52°,
∴∠AOB=360°-90°-90°-52°=128°,
∴∠DOE=∠FOE+∠FOD=$\frac{1}{2}$(∠BOF+∠AOF)=$\frac{1}{2}$∠BOA=64°.
点评 主要考查了切线的性质、切线长定理、勾股定理等几何知识点的应用问题;解题的关键是作辅助线,灵活运用有关定理来分析、判断.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
7.代数式$\frac{{\sqrt{x}}}{x-1}$有意义的条件是( )
| A. | x≠1 | B. | x≥0 | C. | x≥0且x≠1 | D. | 任意实数 |
11.二次函数y=$\frac{1}{2}(x-3)^{2}$的图象的开口方向,对称轴分别是( )
| A. | 向上,直线x=3 | B. | 向下,直线x=3 | C. | 向上,直线x=-3 | D. | 向下,直线x=-3 |
1.计算1$÷\frac{2}{3}×(-\frac{3}{2})$的结果是( )
| A. | -1 | B. | 1 | C. | -$\frac{9}{4}$ | D. | -$\frac{4}{9}$ |
5.函数y=mx+n与y=nx的大致图象是( )
| A. | 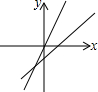 | B. | 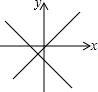 | C. | 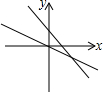 | D. |  |
 若正六边形的边长为8cm,求它的半径、边心距和面积.
若正六边形的边长为8cm,求它的半径、边心距和面积.