Question

13．如图，在矩形ABCD中，把∠B，∠D分别翻折，使点B，D分别落在对角线AC上的点E，F处，折痕分别为CM，AN．
（1）求证：△AND≌△CMB；
（2）连接MF、NE，证明四边形MFNE是平行四边形；四边形MFNE是菱形吗？请说明理由；
（3）点P、Q是矩形的边CD、AB上的两点，连接PQ、CQ、MN，如图2所示，若PQ=CQ，PQ∥MN，且AB=4，BC=3，DN=$\frac{3}{2}$，求PC的长度．

Answer 1

分析 （1）根据折叠的性质得出∠DAN=∠NAC，∠BCM=∠ACM，从而根据AD∥BC可得出∠DAN=∠BCM，从而即可判断出△ADN≌△CBM．
（2）连接NE、MF，根据（1）的结论可得出NF=ME，再由∠NFE=∠MEF可判断出NF∥ME，在直角三角形NFE中，NE为斜边，NF为直角边，可判断四边形MFNE不是菱形．
（3）设AC与MN的交点为O，EF=x，作QG⊥PC于G点，首先求出AC=5，根据翻折变换知：AF=CE=3，于是可得AF+（CE-EF）=5，可得EF=1，在Rt△NFE中，NO²=NF²+OF²，求出NO的长，即NM=PQ=QC=2NO，PC=2$\sqrt{P{Q}^{2}-Q{G}^{2}}$．

解答 （1）证明：∵四边形ABCD是矩形，
∴AD=BC，∠B=∠D=90°，
由折叠的性质得出∠DAN=∠NAC，∠BCM=∠ACM，
∵AD∥BC，
∴∠DAC=∠BCA，
∴∠DAN=∠BCM，
在Rt△AND和Rt△CMB中，$\left\{\begin{array}{l}{∠DAN=∠BCM}&{\;}\\{∠D=∠B}&{\;}\\{AD=BC}&{\;}\end{array}\right.$，
∵∴△AND≌△CMB（AAS）
（2）解：由（1）得：△AND≌△CMB，
∴NF=ME，
∵∠NFE=∠MEF，
∴NF∥ME，
∴四边形MFNE是平行四边形，
∵MN与EF不垂直，
∴四边形MFNE不是菱形；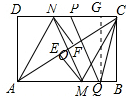
（3）解：设AC与MN的交点为O，EF=x，作QG⊥PC于G点，如图所示：
∵AB=4，BC=3，
∴AC=5，
∵AF=CE=BC=3，
∴2AF-EF=AC，即6-x=5，
解得：x=1，
∴EF=1，
∴CF=2，
由折叠的性质得：NF=DN=$\frac{3}{2}$，
∵OE=OF=$\frac{1}{2}$EF=$\frac{1}{2}$，
∴在Rt△NFO中，ON²=OF²+NF²，
∴ON=$\frac{\sqrt{10}}{2}$，
∴MN=2ON=$\sqrt{10}$，
∵PQ∥MN，PN∥MQ，
∴四边形MQPN是平行四边形，
∴MN=PQ=$\sqrt{10}$，
∵PQ=CQ，
∴△PQC是等腰三角形，
∴PG=CG，
在Rt△QPG中，PG²=PQ²-QG²，
∴PG=$\sqrt{10-9}$=1，
∴PC=2PG=2．

点评 本题是四边形综合题目，考查了翻折变换的性质、正方形的性质、全等三角形的判定与性质、勾股定理、平行四边形的判定与性质、菱形的判定等知识；本题综合性强，有一定难度，熟练掌握折叠的性质和正方形的性质是解决问题的关键．