题目内容
如图1,矩形OABC中,AB=8,OA=4,把矩形OABC对折,使点B与点O重合,点C移到点F位置,折痕为DE.(1)求OD的长;
(2)连接BE,四边形OEBD是什么特殊四边形?请运用所学知识进行说明;
(3)以O点为坐标原点,OC、OA 所在的直线分
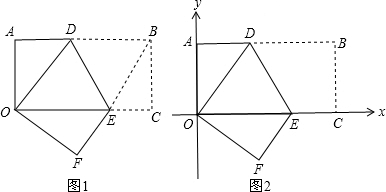 别为x轴、y轴(如图2),求直线EF的函数表达式.
别为x轴、y轴(如图2),求直线EF的函数表达式.
分析:(1)根据折叠的性质得到OD=DB,设OD=x,则DB=x,AD=8-x,利用勾股定理得到x2=(8-x)2+42,解方程即可得到x;
(2)根据折叠的性质得到∠2=∠1,DB=DO,BE=EO,而∠3=∠1,得∠2=∠3,则OD=OE,即可得到四边形OEBD的四边都相等,根据菱形的定义即可判断;
(3)过F作FG⊥x轴于G,根据折叠的性质得OE=OD=5,EC=EF=3,OF=BC=4,∠OFE=∠B=90°,可得E点坐标,利用等积法科求出GF,再利用勾股定理可求得OG,即得到F点坐标,然后根据待定系数法可求得直线EF的函数表达式.
(2)根据折叠的性质得到∠2=∠1,DB=DO,BE=EO,而∠3=∠1,得∠2=∠3,则OD=OE,即可得到四边形OEBD的四边都相等,根据菱形的定义即可判断;
(3)过F作FG⊥x轴于G,根据折叠的性质得OE=OD=5,EC=EF=3,OF=BC=4,∠OFE=∠B=90°,可得E点坐标,利用等积法科求出GF,再利用勾股定理可求得OG,即得到F点坐标,然后根据待定系数法可求得直线EF的函数表达式.
解答: 解:(1)如图1,
解:(1)如图1,
∵矩形OABC对折,使点B与点O重合,点C移到点F位置,
∴OD=DB,
设OD=x,则DB=x,AD=8-x,
在Rt△AOD中,OA=4,
∴OD2=AD2+OA2,即x2=(8-x)2+42,解得x=5,
所以OD的长为5;
(2)四边形OEBD是菱形.理由如下:
∵矩形OABC对折,使点B与点O重合,点C移到点F位置,
∴∠2=∠1,DB=DO,BE=EO,
而∠1=∠3,
∴∠2=∠3,
∴OD=OE,
∴OD=DB=BE=OE,
∴四边形OEBD是菱形;
(3)过F作FG⊥x轴于G,如图2,
∵矩形OABC对折,使点B与点O重合,点C移到点F位置,
∴OE=OD=5,EC=EF=3,OF=BC=4,∠OFE=∠B=90°,
∴E点坐标为(5,0);
∵
OE•GF=
OF•EF,
∴GF=
=
,
在Rt△OFG中,OG=
=
=
,
∴F点坐标为(
,-
),
设直线EF的解析式为y=kx+b,
把E(5,0)和F(
,-
)代入得,5k+b=0,
k+b=-
,解得k=
,b=-
,
∴直线EF的函数表达式为y=
x-
.
 解:(1)如图1,
解:(1)如图1,∵矩形OABC对折,使点B与点O重合,点C移到点F位置,
∴OD=DB,
设OD=x,则DB=x,AD=8-x,
在Rt△AOD中,OA=4,
∴OD2=AD2+OA2,即x2=(8-x)2+42,解得x=5,
所以OD的长为5;
(2)四边形OEBD是菱形.理由如下:
∵矩形OABC对折,使点B与点O重合,点C移到点F位置,
∴∠2=∠1,DB=DO,BE=EO,
而∠1=∠3,
∴∠2=∠3,
∴OD=OE,
∴OD=DB=BE=OE,
∴四边形OEBD是菱形;
(3)过F作FG⊥x轴于G,如图2,

∵矩形OABC对折,使点B与点O重合,点C移到点F位置,
∴OE=OD=5,EC=EF=3,OF=BC=4,∠OFE=∠B=90°,
∴E点坐标为(5,0);
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴GF=
| 3×4 |
| 5 |
| 12 |
| 5 |
在Rt△OFG中,OG=
| OF2-GF2 |
4 2-(
|
| 16 |
| 5 |
∴F点坐标为(
| 16 |
| 5 |
| 12 |
| 5 |
设直线EF的解析式为y=kx+b,
把E(5,0)和F(
| 16 |
| 5 |
| 12 |
| 5 |
| 16 |
| 5 |
| 12 |
| 5 |
| 4 |
| 3 |
| 20 |
| 3 |
∴直线EF的函数表达式为y=
| 4 |
| 3 |
| 20 |
| 3 |
点评:本题考查了利用待定系数法一次函数的解析式:先确定两个点的坐标,然后代入y=kx+b中,得到方程组,解方程组即可.也考查了折叠的性质:折叠前后两图形全等,即对应线段相等,对应角相等;还考查了矩形的性质、菱形的定义以及勾股定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

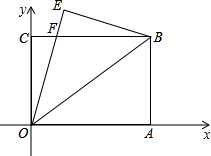 如图,将矩形OABC在直角坐标系中A(4,0),B(4,3),将矩形OABC沿OB对折,使点A落在E处,并交BC于点F,则BF=
如图,将矩形OABC在直角坐标系中A(4,0),B(4,3),将矩形OABC沿OB对折,使点A落在E处,并交BC于点F,则BF= 如图,在矩形OABC中,OA=8,OC=4,OA,OC分别在x,y轴上,点D在OA上,且CD=AD.
如图,在矩形OABC中,OA=8,OC=4,OA,OC分别在x,y轴上,点D在OA上,且CD=AD.
 上的一个动点(不与点O重合).
上的一个动点(不与点O重合).