题目内容
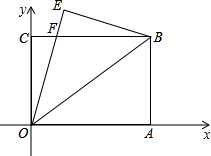 如图,将矩形OABC在直角坐标系中A(4,0),B(4,3),将矩形OABC沿OB对折,使点A落在E处,并交BC于点F,则BF=
如图,将矩形OABC在直角坐标系中A(4,0),B(4,3),将矩形OABC沿OB对折,使点A落在E处,并交BC于点F,则BF=分析:根据折叠的性质和平行线的性质,得∠BOF=∠AOB=∠OBF,则OF=BF;设BF=x,则CF=4-x.根据勾股定理列方程进行求解;作EN⊥OA于N,交BC于M.根据前边的结论,可以求得△BEF的三边,进而根据直角三角形的面积公式求得EM的长,从而求得EN的长,再根据勾股定理求得ON的长即可.
解答: 解:∵OA∥BC,
解:∵OA∥BC,
∴∠OBC=∠AOB.
又∠BOE=∠AOB,
∴∠BOE=∠OBC,
∴OF=BF.
设BF=x,则CF=4-x.
根据勾股定理,得
9+(4-x)2=x2,
解得
x=
.
即BF=
.
作EN⊥OA于N,交BC于M.
在直角三角形BEF中,BE=AB=3,EF=
,BF=
,
∴EM=
.
则EN=3+
=
.
根据勾股定理,得ON=
.
即点E(
,
).
 解:∵OA∥BC,
解:∵OA∥BC,∴∠OBC=∠AOB.
又∠BOE=∠AOB,
∴∠BOE=∠OBC,
∴OF=BF.
设BF=x,则CF=4-x.
根据勾股定理,得
9+(4-x)2=x2,
解得
x=
| 25 |
| 8 |
即BF=
| 25 |
| 8 |
作EN⊥OA于N,交BC于M.
在直角三角形BEF中,BE=AB=3,EF=
| 7 |
| 8 |
| 25 |
| 8 |
∴EM=
| 21 |
| 25 |
则EN=3+
| 21 |
| 25 |
| 96 |
| 25 |
根据勾股定理,得ON=
8
| ||
| 25 |
即点E(
8
| ||
| 25 |
| 96 |
| 25 |
点评:此题考查了矩形的性质、等腰三角形的判定、勾股定理以及直角三角形的性质.
直角三角形斜边上的高等于两条直角边的乘积除以斜边.
直角三角形斜边上的高等于两条直角边的乘积除以斜边.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
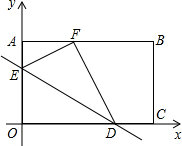 如图,将矩形OABC放置在平面直角坐标系中,点D在边0C上,点E在边OA上,把矩形沿直线DE翻折,使点O落在边AB上的点F处,且tan∠BFD=
如图,将矩形OABC放置在平面直角坐标系中,点D在边0C上,点E在边OA上,把矩形沿直线DE翻折,使点O落在边AB上的点F处,且tan∠BFD=