题目内容
如图,∠DBC=30°,AB=DB,利用此图求tan75°=______.

∵AB=BD,∴∠A=∠ADB.
∵∠DBC=30°=2∠A,
∴∠A=15°,∠ADC=75°.
设CD=x,
∴AB=BD=
=
=2x,
BC=CD×cot∠DBC=
x,
AC=AB+BC=(2+
)x,
∴tan∠ADC=tan75°
=AC:CD
=2+
.
∵∠DBC=30°=2∠A,
∴∠A=15°,∠ADC=75°.
设CD=x,
∴AB=BD=
| CD |
| sin∠DBC |
| x | ||
|
BC=CD×cot∠DBC=
| 3 |
AC=AB+BC=(2+
| 3 |
∴tan∠ADC=tan75°
=AC:CD
=2+
| 3 |

练习册系列答案
相关题目
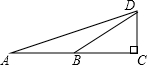 如图,∠DBC=30°,AB=DB,利用此图求tan75°=
如图,∠DBC=30°,AB=DB,利用此图求tan75°=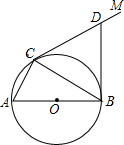 DBC=∠CAB.
DBC=∠CAB. 如图,∠DBC=30°,AB=DB,利用此图求tan75°=________.
如图,∠DBC=30°,AB=DB,利用此图求tan75°=________.