题目内容
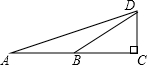 如图,∠DBC=30°,AB=DB,利用此图求tan75°=
如图,∠DBC=30°,AB=DB,利用此图求tan75°=分析:由AB=BD推出∠A=∠ADB,根据三角形的外角等于与它不相邻的两内角和知∠A=15°,∠ADC=75°.设CD=x,表示出AB、BD、BC,进一步表示AC.根据tan∠ADC=tan75°=AC:CD求解.
解答:解:∵AB=BD,∴∠A=∠ADB.
∵∠DBC=30°=2∠A,
∴∠A=15°,∠ADC=75°.
设CD=x,
∴AB=BD=
=
=2x,
BC=CD×cot∠DBC=
x,
AC=AB+BC=(2+
)x,
∴tan∠ADC=tan75°
=AC:CD
=2+
.
∵∠DBC=30°=2∠A,
∴∠A=15°,∠ADC=75°.
设CD=x,
∴AB=BD=
| CD |
| sin∠DBC |
| x | ||
|
BC=CD×cot∠DBC=
| 3 |
AC=AB+BC=(2+
| 3 |
∴tan∠ADC=tan75°
=AC:CD
=2+
| 3 |
点评:此题综合考查了解直角三角形的知识,要求学生有较强逻辑推理能力和运算能力.

练习册系列答案
相关题目
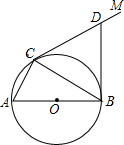 DBC=∠CAB.
DBC=∠CAB. 如图,∠DBC=30°,AB=DB,利用此图求tan75°=________.
如图,∠DBC=30°,AB=DB,利用此图求tan75°=________.
