题目内容
 如图,四边形ABFE中,延长FE至点P,∠AEP=74°,∠BEF=30°,∠EFB=120°,AF平分∠EFB,EF=2.求AB长(结果精确到0.1).
如图,四边形ABFE中,延长FE至点P,∠AEP=74°,∠BEF=30°,∠EFB=120°,AF平分∠EFB,EF=2.求AB长(结果精确到0.1).
(参考数据: ≈1.73,
≈1.73, ≈1.41,sin74°≈0.6,cos74°≈0.28,
≈1.41,sin74°≈0.6,cos74°≈0.28,
tan74°≈3.49,sin76°≈0.97,cos76°≈0.24)
解:∵∠EFB=120°,AF平分∠EFB,
∴∠EFO=60°,∠EOF=90°,
∴FE=FB.
在Rt△EOF中,
∴OE= .
.
Rt△EOA中,
∴AE= ,
,
在△AEF和△ABF中,
 ,
,
∴△AEF≌△ABF,
∴AB=AE=7.2.
分析:先由∠EFB=120°,AF平分∠EFB,得出∠EFO=60°,∠EOF=90°,则FE=FB,再解Rt△EOF,求出OE= ,解Rt△EOA,求出AE≈7.2,然后证明△AEF≌△ABF,即可得到AB=AE=7.2.
,解Rt△EOA,求出AE≈7.2,然后证明△AEF≌△ABF,即可得到AB=AE=7.2.
点评:本题考查了解直角三角形,全等三角形的判定与性质,难度适中,判定△AEF≌△ABF是解题的关键.
∴∠EFO=60°,∠EOF=90°,
∴FE=FB.
在Rt△EOF中,
∴OE=
 .
.Rt△EOA中,
∴AE=
 ,
,在△AEF和△ABF中,
 ,
,∴△AEF≌△ABF,
∴AB=AE=7.2.
分析:先由∠EFB=120°,AF平分∠EFB,得出∠EFO=60°,∠EOF=90°,则FE=FB,再解Rt△EOF,求出OE=
 ,解Rt△EOA,求出AE≈7.2,然后证明△AEF≌△ABF,即可得到AB=AE=7.2.
,解Rt△EOA,求出AE≈7.2,然后证明△AEF≌△ABF,即可得到AB=AE=7.2.点评:本题考查了解直角三角形,全等三角形的判定与性质,难度适中,判定△AEF≌△ABF是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 20、如图,四边形ABFE与四边形EFCD是两个大小一样的正方形,试在图中找出所有能使正方形EFCD按顺时针方向旋转一定的角度后能与正方形ABFE重合的点,并分别说出旋转的度数.
20、如图,四边形ABFE与四边形EFCD是两个大小一样的正方形,试在图中找出所有能使正方形EFCD按顺时针方向旋转一定的角度后能与正方形ABFE重合的点,并分别说出旋转的度数. 23、如图,四边形ABFE和四边形EFCD都是平行四边形,四边形ABCD是平行四边形吗?说明你的理由.
23、如图,四边形ABFE和四边形EFCD都是平行四边形,四边形ABCD是平行四边形吗?说明你的理由.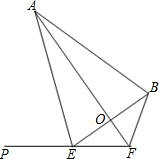 (2013•石景山区二模)如图,四边形ABFE中,延长FE至点P,∠AEP=74°,∠BEF=30°,∠EFB=120°,AF平分∠EFB,EF=2.求AB长(结果精确到0.1).
(2013•石景山区二模)如图,四边形ABFE中,延长FE至点P,∠AEP=74°,∠BEF=30°,∠EFB=120°,AF平分∠EFB,EF=2.求AB长(结果精确到0.1).