题目内容
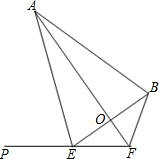 (2013•石景山区二模)如图,四边形ABFE中,延长FE至点P,∠AEP=74°,∠BEF=30°,∠EFB=120°,AF平分∠EFB,EF=2.求AB长(结果精确到0.1).
(2013•石景山区二模)如图,四边形ABFE中,延长FE至点P,∠AEP=74°,∠BEF=30°,∠EFB=120°,AF平分∠EFB,EF=2.求AB长(结果精确到0.1).(参考数据:
| 3 |
| 2 |
tan74°≈3.49,sin76°≈0.97,cos76°≈0.24)
分析:先由∠EFB=120°,AF平分∠EFB,得出∠EFO=60°,∠EOF=90°,则FE=FB,再解Rt△EOF,求出OE=
,解Rt△EOA,求出AE≈7.2,然后证明△AEF≌△ABF,即可得到AB=AE=7.2.
| 3 |
解答:解:∵∠EFB=120°,AF平分∠EFB,
∴∠EFO=60°,∠EOF=90°,
∴FE=FB.
在Rt△EOF中,
∴OE=EFcos30°=
.
Rt△EOA中,
∴AE=
=
≈7.2,
在△AEF和△ABF中,
,
∴△AEF≌△ABF,
∴AB=AE=7.2.
∴∠EFO=60°,∠EOF=90°,
∴FE=FB.
在Rt△EOF中,
∴OE=EFcos30°=
| 3 |
Rt△EOA中,
∴AE=
| OE |
| cos∠AEO |
| ||
| cos76° |
在△AEF和△ABF中,
|
∴△AEF≌△ABF,
∴AB=AE=7.2.
点评:本题考查了解直角三角形,全等三角形的判定与性质,难度适中,判定△AEF≌△ABF是解题的关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
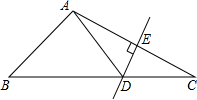 (2013•石景山区二模)如图,△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为14cm,则△ABC的周长为( )
(2013•石景山区二模)如图,△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为14cm,则△ABC的周长为( ) (2013•石景山区二模)如图,AB是⊙O的直径,C是⊙O上的一点,若AC=8,AB=10,OD⊥BC于点D,则BD的长为( )
(2013•石景山区二模)如图,AB是⊙O的直径,C是⊙O上的一点,若AC=8,AB=10,OD⊥BC于点D,则BD的长为( )