题目内容
10.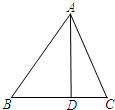 如图所示,已知△ABC中,∠BAC=45°,AD⊥BC于D,BD=2,CD=3,试求AD的长.
如图所示,已知△ABC中,∠BAC=45°,AD⊥BC于D,BD=2,CD=3,试求AD的长.
分析 如图,过B作BE⊥AC,垂足为E交AD于F,由∠BAC=45°可以得到BE=AE,再根据已知条件可以证明△AFE≌△BCE,可以得到AF=BC=10,而∠FBD=∠DAC,又∠BDF=∠ADC=90°,由此可以证明△BDF∽△ADC,所以FD:DC=BD:AD,设FD长为x,则可建立关于x的方程,解方程即可求出FD,AD的长.
解答 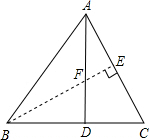 解:如图,过B作BE⊥AC,垂足为E交AD于F,
解:如图,过B作BE⊥AC,垂足为E交AD于F,
∵∠BAC=45°,
∴BE=AE,
∵∠C+∠EBC=90°,∠C+∠EAF=90°,
∴∠EAF=∠EBC,
在△AFE与△BCE中,
$\left\{\begin{array}{l}{∠EAF=∠EBC}\\{BE=AE}\\{∠FEA=∠CEB=90°}\end{array}\right.$,
∴△AFE≌△BCE(ASA),
∴AF=BC=BD+DC=5,∠FBD=∠DAC,
又∵∠BDF=∠ADC=90°,
∴△BDF∽△ADC,
∴FD:DC=BD:AD,
设FD长为x,则
x:2=3:(x+5),
解得x=1,即FD=1,
∴AD=AF+FD=5+1=6.
点评 本题考查了解直角三角形,勾股定理,全等三角形的判定和性质,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
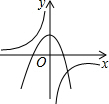
4.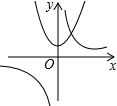 如图,抛物线y=x2+1与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}-{x}^{2}$-1>0的解集是( )
如图,抛物线y=x2+1与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}-{x}^{2}$-1>0的解集是( )
 如图,抛物线y=x2+1与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}-{x}^{2}$-1>0的解集是( )
如图,抛物线y=x2+1与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}-{x}^{2}$-1>0的解集是( )| A. | x>1 | B. | x<-1 | C. | 0<x<1 | D. | -1<x<0 |
19.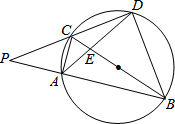 如图所示,BC为圆的直径,图中相似三角形的对数共有( )
如图所示,BC为圆的直径,图中相似三角形的对数共有( )
 如图所示,BC为圆的直径,图中相似三角形的对数共有( )
如图所示,BC为圆的直径,图中相似三角形的对数共有( )| A. | 2对 | B. | 3对 | C. | 4对 | D. | 5对 |
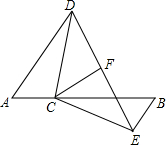 如图,点C在线段AB上,AD∥BE,AC=BE,AD=BC,CF平分∠DCE,
如图,点C在线段AB上,AD∥BE,AC=BE,AD=BC,CF平分∠DCE,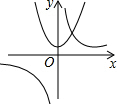
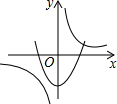
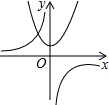
 将形状相同.大小相等的两个长方体小木块按如图所示放置在水平面上,则其主视图是( )
将形状相同.大小相等的两个长方体小木块按如图所示放置在水平面上,则其主视图是( )


