题目内容
11. 如图,在锐角△ABC中,sinB=$\frac{4}{5}$,tanC=2,且S△ABC=10,求BC的长.
如图,在锐角△ABC中,sinB=$\frac{4}{5}$,tanC=2,且S△ABC=10,求BC的长.
分析 过A作AD⊥BC,根据三角函数的定义得到$\frac{AD}{AB}$=$\frac{4}{5}$,$\frac{AD}{CD}$=2,求得$\frac{AD}{BD}=\frac{4}{3}$,于是得到BC=BD+CD=$\frac{5}{4}$AD,根据三角形的面积公式列方程即可得到结论.
解答  解:过A作AD⊥BC,
解:过A作AD⊥BC,
∵sinB=$\frac{4}{5}$,tanC=2,
∴$\frac{AD}{AB}$=$\frac{4}{5}$,$\frac{AD}{CD}$=2,
∴$\frac{AD}{BD}=\frac{4}{3}$,
∴BD=$\frac{3}{4}$AD,CD=$\frac{1}{2}$AD,
∴BC=BD+CD=$\frac{5}{4}$AD,
∵S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}×\frac{5}{4}$•AD2=10,
∴AD=4,
∴BC=5.
点评 本题考查了解直角三角形,三角形面积公式,正确的作出辅助线构造直角三角形是解题的关键.

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
1.已知A,B,C在一条直线上,AB=10,AC=6,那么AB的中点与AC的中点的距离为( )
| A. | 8 | B. | 2或8 | C. | 2 | D. | 6 |
20.某校艺体节上有34个同学同时参加男单、男双乒乓球比赛,正好用了12张球台,问男单、男双各几桌?若设男单x桌,男双y桌,所列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{x+y=34}\\{x-y=12}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=12}\\{x+2y=34}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=12}\\{2x+4y=34}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-y=12}\\{2x+4y=34}\end{array}\right.$ |
 如图,DE∥BC,AD=4cm,DE=2cm,BC=5cm,则AB=10cm.
如图,DE∥BC,AD=4cm,DE=2cm,BC=5cm,则AB=10cm.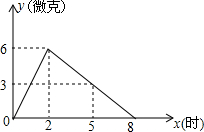 某医药研究所开发了一种新药,在实验药效时发现,如果成人按规定剂量服用,每毫升血液中含药量y(微克)随时间x(时)的变化情况如图所示,那么当成人按规定剂量服药后,根据图象回答下列问题:
某医药研究所开发了一种新药,在实验药效时发现,如果成人按规定剂量服用,每毫升血液中含药量y(微克)随时间x(时)的变化情况如图所示,那么当成人按规定剂量服药后,根据图象回答下列问题: