Question

4．如图，在等边△ABC中，点D在BC上，且BD=$\frac{1}{2}$CD，点E在AB上，点F在AC上，∠EDF=120°．若BE=2CF，且四边形AEDF的面积为$\frac{37\sqrt{3}}{4}$，则EF的长为$\frac{7\sqrt{15}}{5}$．

Answer 1

分析 作EG∥AC交BC于G，FH∥AB交BC于H，易得△BEG，△CFH为等边三角形，利用相似三角形的判定可得△DEG∽△FDH，由相似三角形的性质可得$\frac{GD}{HF}=\frac{GE}{HD}$，设AF=3x，CF=3y，可得AB、BD、CF，易得x、y的关系，再由S_{四边形AEDF}=S_△ABC-S_△BDE-S_△CDF易得y²，再根据勾股定理求出EF．

解答 解：作EG∥AC交BC于G，FH∥AB交BC于H，EM⊥AC于M，
则△BEG，△CFH为等边三角形，
∴∠DGE=120°，∠DHF=120°，
∴∠DGE=∠FHD，
∵∠EDF=120°，
∴∠EDG+∠FDH=60°，
∵∠EDG+∠DEG=60°，
∴DEG=∠FDH，
∴△DEG∽△FDH，
∴$\frac{GD}{HF}=\frac{GE}{HD}$，
设AF=3x，CF=3y，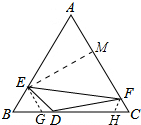
则AB=AC=BC=3x+3y，
∵BD=$\frac{1}{2}$CD，
∴BD=x+y，CF=6y，
∴GD=BD-BG=x+y-6y=x-5y，
HD=CD-CH=2x+2y-3y=2x-y，
∴$\frac{x-5y}{3y}=\frac{6y}{2x-y}$，
x=6.5y，
∵S_{四边形AEDF}=S_△ABC-S_△BDE-S_△CDF
=S_△ABC-$\frac{1}{2}$•BD•EB•sin60°-$\frac{1}{2}$•CD•CF•sin60°
=$\frac{\sqrt{3}}{4}$×[（3x+3y）²-6y（x+y）-3y（2x+2y）]
=$\frac{3\sqrt{3}}{4}$（x+y）（3x-y）=$\frac{3\sqrt{3}}{4}×\frac{15}{2}y×\frac{37}{2}y$=$\frac{37\sqrt{3}}{4}$
∴y²=$\frac{4}{45}$，
∵EF²=EM²+FM²，EM²=AE²-AM²，
∴EF²=AE²-AM²+MF²
∴EF²=（3x-3Y）²-（$\frac{3}{2}x-\frac{3}{2}y$）²+（$\frac{3}{2}$x+$\frac{3}{2}$y）²
=9×$\frac{147}{4}$y²
=9×$\frac{147}{45}$
=$\frac{147}{5}$，
∴EF=$\frac{7\sqrt{15}}{5}$，
故答案为：$\frac{7\sqrt{15}}{5}$．

点评 本题考查等边三角形的性质、相似三角形的判定和性质、勾股定理等知识，解题关键是添加辅助线构造相似三角形，通过巧妙设元利用相似三角形的性质，发现线段之间的关系，本题还体现了转化的思想，有一定的代数化简技巧，属于难题．