题目内容

8．若点（x1，y1），（x2，y2），（x3，y3）都是反比例函数y=-$\frac{1}{x}$图象上的点，并且y1＜0＜y2＜y3，则下列各式中正确的是（　　）
A．x1＜x2＜x3B．x1＜x3＜x2C．x2＜x1＜x3D．x2＜x3＜x1

分析 先根据反比例函数的解析式判断出函数图象所在的象限及在每一象限内函数的增减性，再根据y1＜0＜y2＜y3判断出三点所在的象限，故可得出结论．

解答 解：∵反比例函数y=-$\frac{1}{x}$中k=-1＜0，
∴此函数的图象在二、四象限，且在每一象限内y随x的增大而增大，
∵y1＜0＜y2＜y3，
∴点（x1，y1）在第四象限，（x2，y2）、（x3，y3）两点均在第二象限，
∴x2＜x3＜x1．
故选D．

点评 本题考查的是反比例函数图象上点的坐标特点，先根据题意判断出函数图象所在的象限是解答此题的关键．

练习册系列答案
相关题目
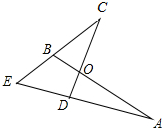18．如图，AB交CD于点O，AD、CB的延长线相交于点E，且OA=OC，EA=EC．你能证明∠A=∠C吗？点O在∠AEC的平分线上吗？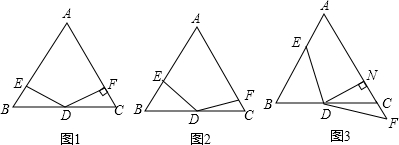
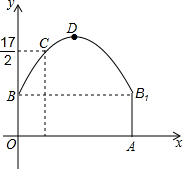19．若（　　）-（-2）=3，则括号内的数是（　　）
A．-1B．1C．5D．-5
16．在△ABC中，AB=AC，∠A=60°，点D是线段BC的中点，∠EDF=120°，DE与线段AB相交于点E．DF与线段AC（或AC的延长线）相交于点F．
（1）如图1，若DF⊥AC，垂足为F，AB=4，求BE的长；
（2）如图2，将（1）中的∠EDF绕点D顺时针旋转一定的角度，DF仍与线段AC相交于点F．求证：BE+CF=$\frac{1}{2}$AB；
（3）如图3，将（2）中的∠EDF继续绕点D顺时针旋转一定的角度，使DF与线段AC的延长线相交于点F，作DN⊥AC于点N，若DN⊥AC于点N，若DN=FN，求证：BE+CF=$\sqrt{3}$（BE-CF）．
3．如图，隧道的截面由抛物线和长方形构成，长方形的长是12m，宽是4m．按照图中所示的直角坐标系，抛物线可以用y=-$\frac{1}{6}$x2+bx+c表示，且抛物线的点C到墙面OB的水平距离为3m时，到地面OA的距离为$\frac{17}{2}$m．
（1）求该抛物线的函数关系式，并计算出拱顶D到地面OA的距离；
（2）一辆货运汽车载一长方体集装箱后高为6m，宽为4m，如果隧道内设双向行车道，那么这辆货车能否安全通过？
（3）在抛物线型拱壁上需要安装两排灯，使它们离地面的高度相等，如果灯离地面的高度不超过8m，那么两排灯的水平距离最小是多少米？
13．-2的倒数是（　　）
A．2B．$\frac{1}{2}$C．-$\frac{1}{2}$D．-2
20．若a、b、c为三角形的三边，且a、b满足$\sqrt{{a}^{2}-9}$+（b-2）2=0，则第三边c的取值范围是1＜c＜5．
17．有四张质地、大小、反面完全相同的不透明卡片，正面分别写着数字1，2，3，4，现把它们的正面向下，随机摆放在桌面上，从中任意抽出一张，则抽出的数字是奇数的概率是$\frac{1}{2}$．
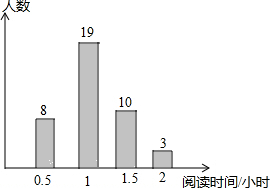18．为响应“书香成都”建设号召，在全校形成良好的人文阅读风尚，成都市某中学随机调查了部分学生平均每天的阅读时间，统计结果如图所示，则在本次调查中，阅读时间的中位数是1小时．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网