题目内容
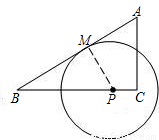
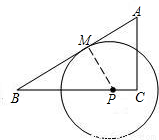
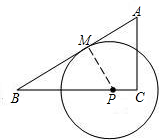
 如图,设△ABC的两边AC与BC之和为a,M是AB的中点,MC=MA=5,则a的取值范围是________.
如图,设△ABC的两边AC与BC之和为a,M是AB的中点,MC=MA=5,则a的取值范围是________.
10<a≤10
分析:根据题设知三角形ABC是直角三角形,由勾股定理求得AB的长度及由三角形的三边关系求得a的取值范围;然后根据题意列出二元二次方程组,通过方程组求得xy的值,再把该值依据根与系数的关系置于一元二次方程z2-az+ =0中,最后由根的判别式求得a的取值范围.
=0中,最后由根的判别式求得a的取值范围.
解答:∵M是AB的中点,MC=MA=5,
∴△ABC为直角三角形,AB=10;
∴a=AC+BC>AB=10;
令AC=x、BC=y.
∴ ,
,
∴xy= ,
,
∴x、y是一元二次方程z2-az+ =0的两个实根,
=0的两个实根,
∴△=a2-4× ≥0,即a≤10
≥0,即a≤10 .综上所述,a的取值范围是10<a≤10
.综上所述,a的取值范围是10<a≤10 .
.
故答案为:10<a≤10 .
.
点评:本题综合考查了勾股定理、直角三角形斜边上的中线及根的判别式.此题的综合性比较强,解题时,还利用了一元二次方程的根与系数的关系、根的判别式的知识点.

分析:根据题设知三角形ABC是直角三角形,由勾股定理求得AB的长度及由三角形的三边关系求得a的取值范围;然后根据题意列出二元二次方程组,通过方程组求得xy的值,再把该值依据根与系数的关系置于一元二次方程z2-az+
 =0中,最后由根的判别式求得a的取值范围.
=0中,最后由根的判别式求得a的取值范围.解答:∵M是AB的中点,MC=MA=5,
∴△ABC为直角三角形,AB=10;
∴a=AC+BC>AB=10;
令AC=x、BC=y.
∴
 ,
,∴xy=
 ,
,∴x、y是一元二次方程z2-az+
 =0的两个实根,
=0的两个实根,∴△=a2-4×
 ≥0,即a≤10
≥0,即a≤10 .综上所述,a的取值范围是10<a≤10
.综上所述,a的取值范围是10<a≤10 .
.故答案为:10<a≤10
 .
.点评:本题综合考查了勾股定理、直角三角形斜边上的中线及根的判别式.此题的综合性比较强,解题时,还利用了一元二次方程的根与系数的关系、根的判别式的知识点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
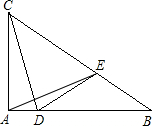 点E沿BC从B向C运动,速度为2cm/秒.动点E到达点C时运动终止.连接DE、CD、AE.
点E沿BC从B向C运动,速度为2cm/秒.动点E到达点C时运动终止.连接DE、CD、AE.